题目内容
函数f（x）=
的定义域为R，则实数a的取值范围是（ ）
| 1 |
| ax2+4x+3 |
A、(-∞，0)∪(0，
| ||
B、(-∞，
| ||
C、[
| ||
D、(
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：函数的定义域是实数，推出分母不为0，对a分类a=0和a≠0讨论利用△＜0，求解即可得到结果．
解答：
解：函数的定义域为R，只需分母不为0即可，
所以a=0时，分母变为4x+3，则当x=-
时，分母为0，定义域不是R，故a≠0，
要使定义域为R，△＜0，16-12a＜0，∴a＞
，
故选：D．
所以a=0时，分母变为4x+3，则当x=-
| 3 |
| 4 |
要使定义域为R，△＜0，16-12a＜0，∴a＞
| 4 |
| 3 |
故选：D．
点评：本题主要考查函数定义域的应用，本类问题主要转化为函数在已知定义域上恒成立问题解决．
练习册系列答案
相关题目
已知α是第三象限角，则
-
=（ ）
|
|
A、
| ||
B、-
| ||
| C、2tanα | ||
D、-
|
已知数列{an}满足an=
（k∈N*），设f(n)=a1+a2+a3+…+a2n-1+a2n，则f（2014）-f（2013）=（ ）
|
| A、42012 |
| B、42013 |
| C、42014 |
| D、42015 |
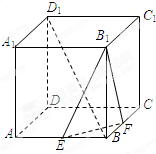如图，在正方体ABCD-A1B1C1D1中，棱AB=1，点E、F分别是AB、BC的中点．
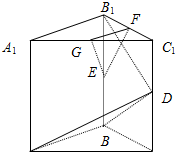在直三棱柱ABCA1B1C1中，∠ABC=90°，BC=2，CC1=4，点E在线段BB1上，且EB1=1，D，F，G分别为CC1，C1B1，C1A1的中点．求证：若点P（-1，-1）在圆x2+y2+4mx-2y+5m=0的外部，则实数m的取值范围为（ ）
| A、（-4，+∞） | ||
B、（-∞，
| ||
C、（-4，
| ||
D、（
|