题目内容
已知数列{an}满足an=
(k∈N*),设f(n)=a1+a2+a3+…+a2n-1+a2n,则f(2014)-f(2013)=( )
|
| A、42012 |
| B、42013 |
| C、42014 |
| D、42015 |
考点:数列的求和
专题:等差数列与等比数列
分析:由数列{an}满足an=
(k∈N*),可得f(n)=a1+a2+a3+…+a2n-1+a2n,f(n-1)=a1+a2+…+a2n-1-1+a2n-1.可得f(n)=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)=[1+3+…+(2n-1)]+f(n-1),利用等差数列的前n项和公式即可得出.
|
解答:
解:∵数列{an}满足an=
(k∈N*),
f(n)=a1+a2+a3+…+a2n-1+a2n,f(n-1)=a1+a2+…+a2n-1-1+a2n-1.
∴f(n)=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)
=[1+3+…+(2n-1)]+f(n-1),
∴f(n)-f(n-1)=
=4n-1.
∴f(2014)-f(2013)=42013.
故选:B.
|
f(n)=a1+a2+a3+…+a2n-1+a2n,f(n-1)=a1+a2+…+a2n-1-1+a2n-1.
∴f(n)=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)
=[1+3+…+(2n-1)]+f(n-1),
∴f(n)-f(n-1)=
| 2n-1×2n |
| 2 |
∴f(2014)-f(2013)=42013.
故选:B.
点评:本题考查了递推式的定义、分段函数的意义、等差数列的前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
函数f(x)=
的定义域为R,则实数a的取值范围是( )
| 1 |
| ax2+4x+3 |
A、(-∞,0)∪(0,
| ||
B、(-∞,
| ||
C、[
| ||
D、(
|
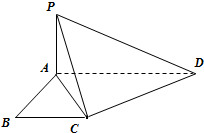 如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.
如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.