题目内容
设二次函数f(x)=ax2+bx+c(a,b,c∈R,a≠0)满足:对称轴为x=-1,且x∈R时x2+x+5≤f(x)≤2x2+5x+9恒成立.
(1)求f(-2)的值;
(2)求函数f(x)的解析式;
(3)已知函数f(x)-kx的图象与x轴交于A,B两点,O为坐标原点,问是否存在实数k满足
=2
?如果存在,求出k的值,如果不存在,请说明理由.
(1)求f(-2)的值;
(2)求函数f(x)的解析式;
(3)已知函数f(x)-kx的图象与x轴交于A,B两点,O为坐标原点,问是否存在实数k满足
| AB |
| OA |
考点:二次函数的性质,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)根据条件:x2+x+5≤f(x)≤2x2+5x+9,便可得到7≤f(-2)≤7,所以便得到f(-2)=7;
(2)根据f(x)的对称轴是x=-1,能够得到f(x-2)=f(-x),从而得到f(0)=f(-2)=7,所以f(x)可设成f(x)=ax(x+2)+7.所以根据x∈R时,x2+x+5≤f(x)可得到(a-1)x2+(2a-1)x+2≥0,所以a需满足
,解该不等式可得a=
,这样便可得f(x)的解析式;
(3)设g(x)=f(x)-kx=
x2+(3-k)x+7,设A(x1,0),B(x2,0),由
=2
可以得到x2=3x1,而x1,x2是方程g(x)=0的两实数根,根据韦达定理即可求出k的值,并验证k是否符合条件即可.
(2)根据f(x)的对称轴是x=-1,能够得到f(x-2)=f(-x),从而得到f(0)=f(-2)=7,所以f(x)可设成f(x)=ax(x+2)+7.所以根据x∈R时,x2+x+5≤f(x)可得到(a-1)x2+(2a-1)x+2≥0,所以a需满足
|
| 3 |
| 2 |
(3)设g(x)=f(x)-kx=
| 3 |
| 2 |
| AB |
| OA |
解答:
解:(1)令x=-2,则7≤f(-2)≤7,所以f(-2)=7;
(2)由f(x)的对称轴为x=-1得,f(x-2)=f(-x),∴f(0)=f(-2)=7;
故可设二次函数f(x)=ax(x+2)+7;
对于x∈R,x2+x+5≤ax2+2ax+7,即(a-1)x2+(2a-1)x+2≥0
则(2a-1)2-8(a-1)≤0且a>1,化简得(2a-3)2≤0,∴a=
;
∴函数f(x)的解析式为f(x)=
x2+3x+7;
(3)设g(x)=f(x)-kx,g(x)=
x2+(3-k)x+7;
设A(x1,0),B(x2,0);
由
=2
有x2=3x1;
∵x1,x2是方程
x2+(3-k)x+7=0的两实数根;
由韦达定理可得,x1+x2=4x1=
,x1x2=3x12=
;
∴x1=±
,
=
;
解得k=3±2
,经检验符合.
(2)由f(x)的对称轴为x=-1得,f(x-2)=f(-x),∴f(0)=f(-2)=7;
故可设二次函数f(x)=ax(x+2)+7;
对于x∈R,x2+x+5≤ax2+2ax+7,即(a-1)x2+(2a-1)x+2≥0
则(2a-1)2-8(a-1)≤0且a>1,化简得(2a-3)2≤0,∴a=
| 3 |
| 2 |
∴函数f(x)的解析式为f(x)=
| 3 |
| 2 |
(3)设g(x)=f(x)-kx,g(x)=
| 3 |
| 2 |
设A(x1,0),B(x2,0);
由
| AB |
| OA |
∵x1,x2是方程
| 3 |
| 2 |
由韦达定理可得,x1+x2=4x1=
| 2k-6 |
| 3 |
| 14 |
| 3 |
∴x1=±
| ||
| 3 |
±4
| ||
| 3 |
| 2k-6 |
| 3 |
解得k=3±2
| 14 |
点评:考查二次函数的对称性,并且由f(x)的对称轴是x=-1能够得到f(x-2)=f(-x),并且设出f(x)=ax(x+2)+7是求解本题的关键,以及韦达定理.

练习册系列答案
相关题目
在△ABC中,|
|=|
|=3,∠ABC=60°,AD是边BC上的高,则
•
的值等于( )
| AB |
| BC |
| AD |
| AC |
A、-
| ||
B、
| ||
C、
| ||
| D、9 |
设有复数ω1=-
+
i,ω2=cos
π+isin
π,令ω=ω1ω2,则复数ω+ω2+ω3+…ω2011=( )
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| A、ω |
| B、ω2 |
| C、ω1 |
| D、ω2 |
| E、ω |
函数f(x)=
的定义域为R,则实数a的取值范围是( )
| 1 |
| ax2+4x+3 |
A、(-∞,0)∪(0,
| ||
B、(-∞,
| ||
C、[
| ||
D、(
|
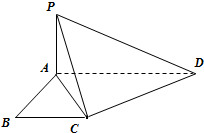 如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.
如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.