题目内容
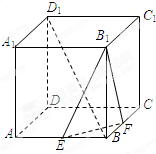 如图,在正方体ABCD-A1B1C1D1中,棱AB=1,点E、F分别是AB、BC的中点.
如图,在正方体ABCD-A1B1C1D1中,棱AB=1,点E、F分别是AB、BC的中点.(Ⅰ)求证:EF⊥BD1;
(Ⅱ)求三棱锥B1-BEF的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)根据直线平面垂直的性质,判定转化证明线线垂直.(Ⅱ)根据体积公式V B1-BEF=
×S△BEF×BB1,先求解面积,高线问题.
| 1 |
| 3 |
解答:
(Ⅰ)证明:连结AC、BD,AC与BD交于点O.
∵DD1⊥AD,DD1⊥AC,AD∩DC=D
∴DD1⊥平面ABCD.
∴DD1⊥AC,
又四边形是正方形,AC⊥BD,BD∩DD1=D
∴AC⊥平面BDD1.
∴AC⊥BD1
∵点E、F分别是AB、BC的中点
∴EF∥AC,
∴EF⊥BD1,
(Ⅱ)解:∵AB=1.BB1⊥平面ABCD,
∴BB1是三棱锥B1-BEF的高,
∵AB⊥BC,E,F,分别是AB,CD的中点.
∴S△BEF=
×BE×BF=
,
∴V B1-BEF=
×S△BEF×BB1=
,
∵DD1⊥AD,DD1⊥AC,AD∩DC=D
∴DD1⊥平面ABCD.
∴DD1⊥AC,
又四边形是正方形,AC⊥BD,BD∩DD1=D
∴AC⊥平面BDD1.
∴AC⊥BD1
∵点E、F分别是AB、BC的中点
∴EF∥AC,
∴EF⊥BD1,
(Ⅱ)解:∵AB=1.BB1⊥平面ABCD,
∴BB1是三棱锥B1-BEF的高,
∵AB⊥BC,E,F,分别是AB,CD的中点.
∴S△BEF=
| 1 |
| 2 |
| 1 |
| 8 |
∴V B1-BEF=
| 1 |
| 3 |
| 1 |
| 24 |
点评:本题考查了直线平面的位置关系,运用定理判断位置关系,求解大小,属于难题.

练习册系列答案
相关题目
已知集合M={-3,-1,1,3},N={-3,0,2,4},则M∩N=( )
| A、∅ |
| B、{-3} |
| C、{-3,3} |
| D、{-3,-2,0,1,2} |
在△ABC中,|
|=|
|=3,∠ABC=60°,AD是边BC上的高,则
•
的值等于( )
| AB |
| BC |
| AD |
| AC |
A、-
| ||
B、
| ||
C、
| ||
| D、9 |
设有复数ω1=-
+
i,ω2=cos
π+isin
π,令ω=ω1ω2,则复数ω+ω2+ω3+…ω2011=( )
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| A、ω |
| B、ω2 |
| C、ω1 |
| D、ω2 |
| E、ω |
函数f(x)=
的定义域为R,则实数a的取值范围是( )
| 1 |
| ax2+4x+3 |
A、(-∞,0)∪(0,
| ||
B、(-∞,
| ||
C、[
| ||
D、(
|