Question

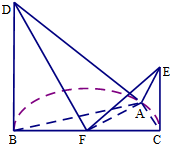如图，BC是半圆F的直径，点A在半圆F上，BC=4

2

，AB=BD=4，BD垂直于半圆F所在在的平面，EC∥DB，且EC=

1

2

DB．
（1）求证：DF⊥平面AEF；
（2）求DA与平面AEF所成的角；
（3）求二面角B-AF-E的余弦值．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的判定,直线与平面所成的角

专题：计算题,证明题,空间位置关系与距离,空间角

分析：（1）运用解直角三角形知识，可得DF⊥EF，再由勾股定理的逆定理，可得DF⊥AF，再由线面垂直的判定定理，即可得证；
（2）由线面所成角的定义，可得∠DAF即为DA与平面AEF所成的角，通过解直角三角形ADF，即可得到；
（3）在△ACF中，过C作CH⊥AF，交于H，连接EH，由线面垂直的性质和判定，可得∠EHC的补角即为二面角B-AF-E的平面角，通过解直角三角形，即可得到所求值．

解答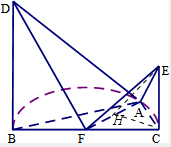： （1）证明：由于EC∥BD，BD⊥平面ABC，则BD⊥BC，EC⊥BC，
由于tan∠DFB=

BD

BF

=

4

2 2

=

2

，tan∠CFE=

EC

CF

=

2

2 2

=

2

2

，
则tan∠DFB•tan∠CFE=1，即有∠DFB+∠EFC=90°，则∠DFE=90°，即DF⊥EF
在直角△ABC中，AF=2

2

，而DF=

16+8

=2

6

，AD=

16+16

=4

2

，
则有DF⊥AF，
有线面垂直判定定理得，DF⊥平面AEF；
（2）解：由于DF⊥平面AEF，则∠DAF即为DA与平面AEF所成的角，
在直角三角形ADF中，AD=4

2

，AF=2

2

，则cos∠DAF=

2 2

4 2

=

1

2

，
即有∠DAF=60°，则DA与平面AEF所成的角为60°；
（3）解：在△ACF中，过C作CH⊥AF，交于H，连接EH，
由于EC⊥平面ABC，则EC⊥AF，即有AF⊥平面ECH，
即有AF⊥EH，∠EHC的补角即为二面角B-AF-E的平面角，
在三角形ACF中，CH=4sin45°=2

2

，
在直角三角形ECH中，EH=

EC2+CH2

=2

3

，
cos∠EHC=

CH

EH

=

2 2

2 3

=

6

3

．
即有二面角B-AF-E的余弦值为-

6

3

．

点评：本题考查空间线面垂直的性质和判定定理及运用，考查直线和平面所成角的求法，和二面角的平面角的求法，考查运算能力，属于中档题．