题目内容
已知函数y=f(x)的定义域是[0,
],求函数y=f(sin2x)的定义域.
| 1 |
| 4 |
考点:函数的定义域及其求法
专题:三角函数的图像与性质
分析:根据抽象函数的定义域可得0≤sin2x≤
,继而得到y=f(sin2x)的定义域.
| 1 |
| 4 |
解答:
解:y=f(x)的定义域是[0,
],
∴0≤sin2x≤
,
∴-
≤sinx≤
,
∴sin(-
)≤sinx≤sin
,
∴-
+2kπ≤x≤
+2kπ,k∈z
故函数y=f(sin2x)的定义域为{x|-
+2kπ≤x≤
+2kπ,k∈z}
| 1 |
| 4 |
∴0≤sin2x≤
| 1 |
| 4 |
∴-
| 1 |
| 2 |
| 1 |
| 2 |
∴sin(-
| π |
| 6 |
| π |
| 6 |
∴-
| π |
| 6 |
| π |
| 6 |
故函数y=f(sin2x)的定义域为{x|-
| π |
| 6 |
| π |
| 6 |
点评:本题考查了抽象函数的定义域,以及三角函数的定义域,属于基础题

练习册系列答案
相关题目
已知变量x,y满足约束条件
,则目标函数z=y-2x的最小值为( )
|
| A、-5 | B、-4 | C、-3 | D、-2 |
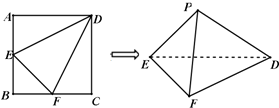 如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△CFD分别沿DE,EF,DF折起,使A,B,C三点重合于点P.
如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△CFD分别沿DE,EF,DF折起,使A,B,C三点重合于点P.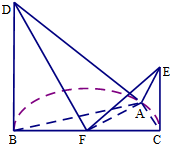 如图,BC是半圆F的直径,点A在半圆F上,BC=4
如图,BC是半圆F的直径,点A在半圆F上,BC=4