题目内容
在正项等比数列{an}中3a1，
a3，2a2成等差数列，则
等于（ ）
| 1 |
| 2 |
| a2013+a2014 |
| a2011+a2012 |
| A、3或-1 | B、9或1 | C、1 | D、9 |
考点：等比数列的性质,等差数列的性质
专题：等差数列与等比数列
分析：由题意可得公比q的方程，解方程可得q，而要求的式子可化为
，代值计算可得．
| q2+q3 |
| 1+q |
解答：
解：∵在正项等比数列{an}中3a1，
a3，2a2成等差数列，
∴3a1+2a2=a3，即3a1+2a1q=a1q2，解得q=3，（q为数列公比）
∴
=
=
=9．
故选：D
| 1 |
| 2 |
∴3a1+2a2=a3，即3a1+2a1q=a1q2，解得q=3，（q为数列公比）
∴
| a2013+a2014 |
| a2011+a2012 |
| a1q2012+a1q2013 |
| a1q2010+a1q2011 |
| q2+q3 |
| 1+q |
故选：D
点评：本题考查等差数列和等比数列，得出等比数列的公比是解决问题的关键，属基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
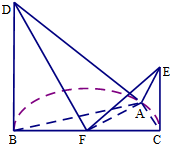如图，BC是半圆F的直径，点A在半圆F上，BC=4