题目内容
已知函数f(x)=cos(
x+
)
(1)f(x)=-
,求角x的集合;
(2)f(x)≥
,求角x的集合;
(3)作出f(x)在[0,2π]的图象.
| 1 |
| 2 |
| π |
| 3 |
(1)f(x)=-
| ||
| 2 |
(2)f(x)≥
| 1 |
| 2 |
(3)作出f(x)在[0,2π]的图象.
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:(1)首先,结合余弦函数的图象求解,即
x+
=
+2kπ或
x+
=
+2kπ,k∈Z,然后,求解即可;
(2)直接解不等式即可;
(3)可以根据“五点法”画出简图.
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
(2)直接解不等式即可;
(3)可以根据“五点法”画出简图.
解答:
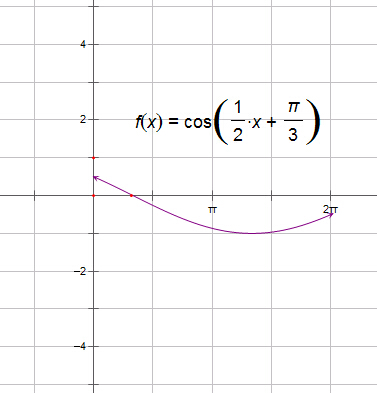 解:(1)∵函数f(x)=cos(
解:(1)∵函数f(x)=cos(
x+
),
∴cos(
x+
)=-
,
∴
x+
=
+2kπ,或
x+
=
+2kπ,k∈Z,
∴x=
+4kπ或x=2π+4kπ,k∈Z,
∴角x的集合{x|x=
+4kπ或x=2π+4kπ,k∈Z};
(2)∵f(x)≥
,
∴-
+2kπ≤
x+
≤
+2kπ,
∴-
+4kπ≤x≤4kπ,
∴角x的集合{x|-
+4kπ≤x≤4kπ,k∈Z};
(3)f(x)在[0,2π]的图象如下图所示:
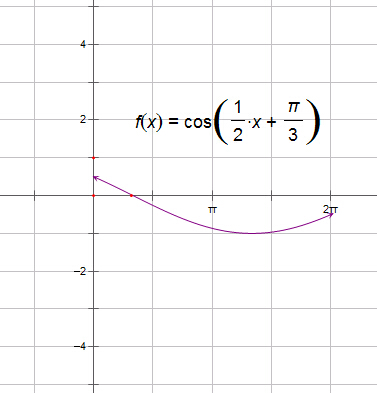 解:(1)∵函数f(x)=cos(
解:(1)∵函数f(x)=cos(| 1 |
| 2 |
| π |
| 3 |
∴cos(
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
∴
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 4π |
| 3 |
∴x=
| 2π |
| 3 |
∴角x的集合{x|x=
| 2π |
| 3 |
(2)∵f(x)≥
| 1 |
| 2 |
∴-
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
∴-
| 4π |
| 3 |
∴角x的集合{x|-
| 4π |
| 3 |
(3)f(x)在[0,2π]的图象如下图所示:
点评:本题重点考查了三角函数的图象与性质,属于中档题.解题关键是熟悉三角函数的图象与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
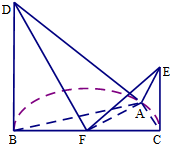 如图,BC是半圆F的直径,点A在半圆F上,BC=4
如图,BC是半圆F的直径,点A在半圆F上,BC=4 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.