题目内容
在△ABC中,
<B<π,AB=
,BC=3,sinC=
.
(1)求sinA的值;
(2)求△ABC的面积.
| π |
| 2 |
| 5 |
| ||
| 6 |
(1)求sinA的值;
(2)求△ABC的面积.
考点:正弦定理的应用,三角形的面积公式
专题:解三角形
分析:(1)利用正弦定理即可得出;
(2)利用同角三角函数基本关系式可得cosA,cosC,再利用两角和差的余弦公式可得cosB,sinB,利用三角形的面积计算公式
acsinB即可得出.
(2)利用同角三角函数基本关系式可得cosA,cosC,再利用两角和差的余弦公式可得cosB,sinB,利用三角形的面积计算公式
| 1 |
| 2 |
解答:
解:(1)由正弦定理可得:
=
,
∴sinA=
=
=
.
(2)∵
<B<π,∴A,C都为锐角,
∴cosA=
=
.
cosC=
=
.
∴cosB=-cos(A+C)=-(cosAcosC-sinAsinC)
=-(
×
-
×
)=
.
∴sinB=
=
.
∴△ABC的面积=
acsinB=
×3×
×
=
.
| a |
| sinA |
| c |
| sinC |
∴sinA=
| asinC |
| c |
3×
| ||||
|
| ||
| 10 |
(2)∵
| π |
| 2 |
∴cosA=
| 1-sin2A |
3
| ||
| 10 |
cosC=
| 1-sin2C |
| 5 |
| 6 |
∴cosB=-cos(A+C)=-(cosAcosC-sinAsinC)
=-(
3
| ||
| 10 |
| 5 |
| 6 |
| ||
| 10 |
| ||
| 6 |
| ||
| 15 |
∴sinB=
| 1-cos2B |
2
| ||
| 15 |
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
2
| ||
| 15 |
| 11 |
点评:本题考查了正弦定理、同角三角函数基本关系式、两角和差的余弦公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
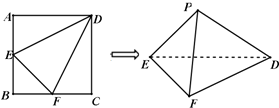 如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△CFD分别沿DE,EF,DF折起,使A,B,C三点重合于点P.
如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△CFD分别沿DE,EF,DF折起,使A,B,C三点重合于点P.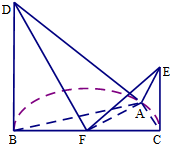 如图,BC是半圆F的直径,点A在半圆F上,BC=4
如图,BC是半圆F的直径,点A在半圆F上,BC=4