题目内容
已知向量
,
的夹角为120°,|
|=2,且
•
=-8,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| b |
| A、6 | B、7 | C、8 | D、9 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据两个向量的数量积表示两个向量的夹角,代入计算即可.
解答:
解:∵cos<
,
>=
,
∴cos120°=
,
解得|
|=8,
故选:C
| a |
| b |
| ||||
|
|
∴cos120°=
| -8 | ||
2×|
|
解得|
| b |
故选:C
点评:本题主要考查用两个向量的数量积表示两个向量的夹角,求向量的模的方法,属于基础题

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知变量x,y满足约束条件
,则目标函数z=y-2x的最小值为( )
|
| A、-5 | B、-4 | C、-3 | D、-2 |
函数y=sinx-tanx的图象大致是( )
A、 |
B、 |
C、 |
D、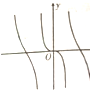 |
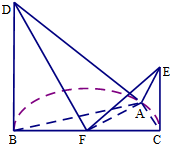 如图,BC是半圆F的直径,点A在半圆F上,BC=4
如图,BC是半圆F的直径,点A在半圆F上,BC=4