题目内容
已知“x2-x-2>0”是“2x+p>0”的必要条件,则实数p的取值范围是 .
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:利用不等式的性质,结合必要条件的定义即可得到结论.
解答:
解:由2x+p>0,得x>-
,即A={x|x>-
},
由x2-x-2>0,解得x>2或x<-1,令B={x|x>2或x<-1},
由题意知A⊆B时,
即-
≥2,
解得p≤-4,
∴实数p的取值范围是(-∞,-4].
故答案为:(-∞,-4].
| p |
| 2 |
| p |
| 2 |
由x2-x-2>0,解得x>2或x<-1,令B={x|x>2或x<-1},
由题意知A⊆B时,
即-
| p |
| 2 |
解得p≤-4,
∴实数p的取值范围是(-∞,-4].
故答案为:(-∞,-4].
点评:本题主要考查充分条件和必要条件的应用,利用不等式的性质求出不等式的等价条件是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数y=2x-2+3的图象恒过点P,则点P为( )
| A、(2,3) |
| B、(1,1) |
| C、(0,1) |
| D、(2,4) |
先后抛掷一枚质地均匀的硬币3次,有2次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
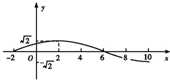 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< 设函数f(x)=|x2-4x-5|.
设函数f(x)=|x2-4x-5|.