题目内容
 设函数f(x)=|x2-4x-5|.
设函数f(x)=|x2-4x-5|.(1)在区间[-2,6]上画出函数f(x)的图象;
(2)设集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞).试判断集合A和B之间的关系,并给出证明;
(3)当k>2时,求证:在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
考点:函数奇偶性的判断,函数的图象
专题:函数的性质及应用
分析:(1)函数f(x)=|x2-4x-5|的图象如图.
(2)方程f(x)=5的解分别是2-
,0,4和2+
,结合函数的单调性求得A,从而得到A B的关系.
(3)当x∈[-1,5]时,令g(x)=k(x+3)-(-x2+4x+5)=(x-
)2-
,根据k>2,分
<1、
<-1,两种情况,分别求得g(x)min >0,从而得出结论.
(2)方程f(x)=5的解分别是2-
| 14 |
| 14 |
(3)当x∈[-1,5]时,令g(x)=k(x+3)-(-x2+4x+5)=(x-
| 4-k |
| 2 |
| k2-20k+36 |
| 4 |
| 4-k |
| 2 |
| 4-k |
| 2 |
解答:
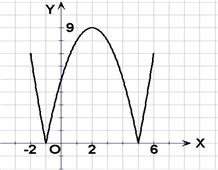 解:(1)函数f(x)=|x2-4x-5|的图象如图:
解:(1)函数f(x)=|x2-4x-5|的图象如图:
(2)方程f(x)=5的解分别是2-
,0,4和2+
,
由于f(x)在(-∞,-1]和[2,5]上单调递减,
在[-1,2]和[5,+∞)上单调递增,
因此,A=( -∞, 2-
] ∪[ 0, 4 ]∪[ 2+
, +∞ ).
由于2+
<6,2-
>-2,
∴B?A.
(3)当x∈[-1,5]时,f(x)=-x2+4x+5.
令g(x)=k(x+3)-(-x2+4x+5)=x2+(k-4)x+(3k-5)=(x-
)2-
,
∵k>2,∴
<1.
又-1≤x≤5,①当-1≤
<1,即2<k≤6时,取x=
,
g(x)min=-
=-
[(k-10)2-64].
∵16≤(k-10)2<64,
∴(k-10)2-64<0,则g(x)min>0.
②当
<-1,即k>6时,取x=-1,g(x)min=2k>0.
由 ①、②可知,当k>2时,g(x)>0,x∈[-1,5].
因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.
 解:(1)函数f(x)=|x2-4x-5|的图象如图:
解:(1)函数f(x)=|x2-4x-5|的图象如图:(2)方程f(x)=5的解分别是2-
| 14 |
| 14 |
由于f(x)在(-∞,-1]和[2,5]上单调递减,
在[-1,2]和[5,+∞)上单调递增,
因此,A=( -∞, 2-
| 14 |
| 14 |
由于2+
| 14 |
| 14 |
∴B?A.
(3)当x∈[-1,5]时,f(x)=-x2+4x+5.
令g(x)=k(x+3)-(-x2+4x+5)=x2+(k-4)x+(3k-5)=(x-
| 4-k |
| 2 |
| k2-20k+36 |
| 4 |
∵k>2,∴
| 4-k |
| 2 |
又-1≤x≤5,①当-1≤
| 4-k |
| 2 |
| 4-k |
| 2 |
g(x)min=-
| k2-20k+36 |
| 4 |
| 1 |
| 4 |
∵16≤(k-10)2<64,
∴(k-10)2-64<0,则g(x)min>0.
②当
| 4-k |
| 2 |
由 ①、②可知,当k>2时,g(x)>0,x∈[-1,5].
因此,在区间[-1,5]上,y=k(x+3)的图象位于函数f(x)图象的上方.
点评:本题主要考查作函数的图象,集合间的关系,函数的恒成立问题,体现了转化的数学思想,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
一个平面将空间分成两部分,两个平面将空间最多分成四部分,三个平面最多将空间分成八部分,…,由此猜测n(n∈N+)个平面最多将空间分成( )
| A、2n部分 | ||
| B、n2部分 | ||
| C、2n部分 | ||
D、
|
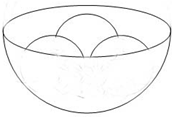 如图,三个半径都是10cm的小球放在一个半球面的碗中,小球的顶端恰好与碗的上沿处于同于水平面,则这个碗的半径R是
如图,三个半径都是10cm的小球放在一个半球面的碗中,小球的顶端恰好与碗的上沿处于同于水平面,则这个碗的半径R是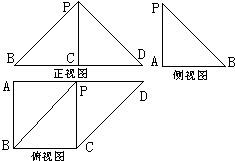 如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )