题目内容
cos42°sin78°+cos48°sin12° ．
考点：两角和与差的正弦函数
专题：计算题,三角函数的求值
分析：利用诱导公式与两角和的正弦公式即可求得cos42°sin78°+cos48°sin12°的值．
解答：
解：∵42°+48°=90°，78°+12°=90°，
∴cos42°sin78°+cos48°sin12°
=cos42°sin78°+sin42°cos78°
=sin（78°+42°）
=sin120°
=
．
故答案为：
．
∴cos42°sin78°+cos48°sin12°
=cos42°sin78°+sin42°cos78°
=sin（78°+42°）
=sin120°
=
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查诱导公式与两角和的正弦公式，考查转化思想与运算求解能力，属于中档题．
练习册系列答案
相关题目
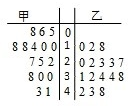甲乙两组统计数据用茎叶图表示，设甲乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等比数列{an}中，a1+a2=8，a3-a1=16，则a3等于（ ）
| A、20 | B、18 | C、10 | D、8 |
已知函数f(x)=sinωx+
cos(π-ωx)（ω＞0）的图象的两相邻对称轴间的距离为
，则f（x）的单调递增区间是（ ）
| 3 |
| π |
| 2 |
A、[kπ-
| ||||
B、[2kπ-
| ||||
C、[kπ-
| ||||
D、[2kπ-
|