题目内容
先后抛掷一枚质地均匀的硬币3次,有2次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:硬币每次正面朝上都概率都为
,由独立重复事件的概率可得.
| 1 |
| 2 |
解答:
解:掷一枚质地均匀的硬币每次正面朝上都概率都为
,
∴有2次正面朝上的概率P=
(
)(
)2=
故选:B
| 1 |
| 2 |
∴有2次正面朝上的概率P=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
故选:B
点评:本题考查古典概型的概率公式,涉及独立重复事件发生的概率,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线
x-3y+2=0和直线
x+y-1=0的倾斜角分别为α,β,tan(α+β)=( )
| 3 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
sin(-585°)的值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知函数f(x)=sinωx+
cos(π-ωx)(ω>0)的图象的两相邻对称轴间的距离为
,则f(x)的单调递增区间是( )
| 3 |
| π |
| 2 |
A、[kπ-
| ||||
B、[2kπ-
| ||||
C、[kπ-
| ||||
D、[2kπ-
|
二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
| A、{x|x>3或x<-2} |
| B、{x|x>2或x<-3} |
| C、{x|-2<x<3} |
| D、{x|-3<x<2} |
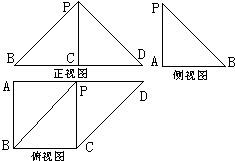 如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )