题目内容
若以连续掷两次骰子分别得到的点数m,n 作为P点的坐标,则点P落在圆x2+y2=14内的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:连续掷两次骰子,得36个P点坐标,由点P落在圆x2+y2=14内,知m2+n2<14,由此能求出点P落在圆x2+y2=14内的概率.
解答:
解:连续掷两次骰子,得P点坐标为:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
总共有36种,
∵点P落在圆x2+y2=14内,∴m2+n2<14,
满足条件的点有:
(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),
共有8个,
∴点P落在圆x2+y2=14内的概率P=
=
.
故答案为:
.
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
总共有36种,
∵点P落在圆x2+y2=14内,∴m2+n2<14,
满足条件的点有:
(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),
共有8个,
∴点P落在圆x2+y2=14内的概率P=
| 8 |
| 36 |
| 2 |
| 9 |
故答案为:
| 2 |
| 9 |
点评:本题考查古典概型及其概率的计算公式的应用,是基础题,解题时要注意列举法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
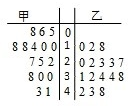 甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为
甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个平面将空间分成两部分,两个平面将空间最多分成四部分,三个平面最多将空间分成八部分,…,由此猜测n(n∈N+)个平面最多将空间分成( )
| A、2n部分 | ||
| B、n2部分 | ||
| C、2n部分 | ||
D、
|
直线
x-3y+2=0和直线
x+y-1=0的倾斜角分别为α,β,tan(α+β)=( )
| 3 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
| A、{x|x>3或x<-2} |
| B、{x|x>2或x<-3} |
| C、{x|-2<x<3} |
| D、{x|-3<x<2} |