题目内容
复数z1=3+4i,z2=1-i,z3=c+(c-2)i(其中i为虚数单位)在复平面内对应的点分别为A、B、C.
(1)若∠BAC是锐角,求实数c的取值范围;
(2)若复数z满足|z-z1|=1,求|z-z2|的取值范围.
(1)若∠BAC是锐角,求实数c的取值范围;
(2)若复数z满足|z-z1|=1,求|z-z2|的取值范围.
考点:复数的代数表示法及其几何意义,复数代数形式的混合运算
专题:数系的扩充和复数
分析:(1)找到复数在复平面内的对应点,∠BAC是锐角,则向量
•
>0,化简即可.
(2)z对应的点在以(3,4)点为圆心,以1为半径的圆上,|z1-z2|=2
,则|z-z2|的最小值为2
-1,最小值为2
+1,进而得到其范围.
| AB |
| AC |
(2)z对应的点在以(3,4)点为圆心,以1为半径的圆上,|z1-z2|=2
| 5 |
| 5 |
| 5 |
解答:
解:(1)由题意得:则A(3,4),B(1,-1),C(c,c-2),
∴
=(-2,-5),
=(c-3,c-6),
∵∠BAC是锐角,
∴
•
>0,
即-2(c-3)-5(c-6)>0,
∴c<
.
又由c=1时,
与
同向,此时夹角为0,
故实数c的取值范围为c<
,且c≠1.
(2)若复数z满足|z-z1|=1,则
z对应的点在以(3,4)点为圆心,以1为半径的圆上,
又由|z1-z2|=
=2
,
故2
-1≤|z-z2|≤2
+1
∴
| AB |
| AC |
∵∠BAC是锐角,
∴
| AB |
| AC |
即-2(c-3)-5(c-6)>0,
∴c<
| 36 |
| 7 |
又由c=1时,
| AB |
| AC |
故实数c的取值范围为c<
| 36 |
| 7 |
(2)若复数z满足|z-z1|=1,则
z对应的点在以(3,4)点为圆心,以1为半径的圆上,
又由|z1-z2|=
| (3-1)2+(4+1)2 |
| 5 |
故2
| 5 |
| 5 |
点评:本题考查复数和向量的对应关系,余弦定理,复数代数形式的运算,是中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
设A1,A2,…,An是平面上的n个不同的点,则满足
+
+…+
=
的点M的个数为( )
| MA1 |
| MA2 |
| MAn |
| 0 |
| A、0 | B、1 | C、2 | D、3 |
“等式sin(α+γ)=sin2β成立”是“α,β,γ成等差数列”的( )条件.
| A、充分而不必要 |
| B、必要而不充分 |
| C、充分必要 |
| D、既不充分又不必要 |
设a,b是实数,则“|b|>|a|>0”是“
>1”的( )
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
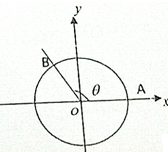 如图A,B是单位圆O上的点,点A是单位圆与x轴正半轴的交点.点B在第二象限,∠AOB=θ,sinθ=
如图A,B是单位圆O上的点,点A是单位圆与x轴正半轴的交点.点B在第二象限,∠AOB=θ,sinθ=