Question

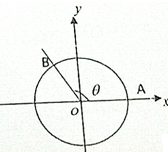如图A，B是单位圆O上的点，点A是单位圆与x轴正半轴的交点．点B在第二象限，∠AOB=θ，sinθ=

4

5

．
（Ⅰ）求B点坐标；
（Ⅱ）求sin（π-θ）+2sin（

π

2

-θ）的值．

Answer 1

考点：运用诱导公式化简求值,单位圆与周期性

专题：三角函数的求值

分析：（1）根据角θ的终边与单位交点为（cosθ，sinθ），结合同角三角函数关系和sinθ=

4

5

，可得B点坐标；
（2）由（1）中结论，结合诱导公式化简，代入可得答案．

解答： 解：（1）∵点A是单位圆与x轴正半轴的交点，点B在第二象限．
设B点坐标为（x，y），
则y=sinθ=

4

5

．
x=-

1-sin2θ

=-

3

5

，
即B点坐标为：（-

3

5

，

4

5

）
（2）sin（π-θ）+2sin（

π

2

-θ）=sinθ+2cosθ=

4

5

+2×(-

3

5

)=-

2

5

．

点评：本题考查的知识点是同角三角函数基本关系的运用，诱导公式，难度不大，属于基本知识的考查．