题目内容
“等式sin（α+γ）=sin2β成立”是“α，β，γ成等差数列”的（ ）条件．
| A、充分而不必要 |
| B、必要而不充分 |
| C、充分必要 |
| D、既不充分又不必要 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据等差数列的性质以及充分条件和必要条件的定义进行判断即可．
解答：
解：若“α，β，γ成等差数列”，则α+γ=2β，此时等式sin（α+γ）=sin2β成立，
若当α=β=0，γ=π，满足sin（α+γ）=sin2β=0，但“α，β，γ成等差数列”不成立，
故“等式sin（α+γ）=sin2β成立”是“α，β，γ成等差数列”的必要不充分条件，
故选：B
若当α=β=0，γ=π，满足sin（α+γ）=sin2β=0，但“α，β，γ成等差数列”不成立，
故“等式sin（α+γ）=sin2β成立”是“α，β，γ成等差数列”的必要不充分条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，根据等差数列的定义和关系是解决本题的关键．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
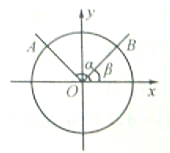在平面直角坐标系xOy内作单位圆O，以Ox为始边作角α、β，它们的终边与单位圆O的交点为A，B，则