题目内容
设a，b是实数，则“|b|＞|a|＞0”是“
＞1”的（ ）
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的关系结合充分条件和必要条件的定义进行判断即可．
解答：
解：若
＞1，则a，b同号，则不等式等价为|
|＞1，即|b|＞|a|＞0，则必要性成立，
若b=-2，a=1，满足|b|＞|a|＞0，但
＞1不成立，则充分性不成立，
故“|b|＞|a|＞0”是“
＞1”的必要不充分条件，
故选：B
| b |
| a |
| b |
| a |
若b=-2，a=1，满足|b|＞|a|＞0，但
| b |
| a |
故“|b|＞|a|＞0”是“
| b |
| a |
故选：B
点评：本题主要考查根据充分条件和必要条件的判断，根据不等式之间的关系是解决本题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
一个等比数列{an}共有2n+1项，奇数项之积为100，偶数项之积为120，则an+1为（ ）
A、
| ||
B、
| ||
| C、20 | ||
| D、110 |
“a＞b＞0”是“a2＞b2”成立的（ ）条件．
| A、必要不充分 |
| B、充分不必要 |
| C、充要 |
| D、既不充分也不必要 |
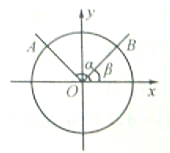在平面直角坐标系xOy内作单位圆O，以Ox为始边作角α、β，它们的终边与单位圆O的交点为A，B，则