题目内容
若p是q的逆否命题，S是q的否命题，则p是S的（ ）
| A、逆命题 | B、原命题 |
| C、否命题 | D、逆否命题 |
考点：四种命题
专题：概率与统计
分析：利用四种命题之间的关系进行判断即可．
解答：
解：设命题p的条件为m，结论为n，则p：m⇒n，p是q的逆否命题，则q：￢n⇒￢m，
因为S是q的否命题，所以S：n⇒m．
所以p是S的逆命题．
故选：A．
因为S是q的否命题，所以S：n⇒m．
所以p是S的逆命题．
故选：A．
点评：本题主要考查四种命题之间的关系，可以根据定义分别判断命题条件和结论之间的变化关系即可．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知平面向量
=（4，1），
=（x，-2），且2
+
与3
-4
平行，则x=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、8 | ||
B、-
| ||
| C、-8 | ||
D、
|
下列函数中，在区间（0，
）上为增函数的是（ ）
| π |
| 2 |
| A、y=sin2x |
| B、y=cosx |
| C、y=-cos2x |
| D、y=-tanx |
若方程
+
=1表示的图形是双曲线，则k的取值范围为（ ）
| x2 |
| 2-k |
| y2 |
| k-1 |
| A、k＞2或k＜1 |
| B、1＜k＜2 |
| C、-2＜k＜1 |
| D、-1＜k＜2 |
设双曲线
-
=1上一点P，F1，F2是焦点，若|PF1|=10，则|PF2|等于（ ）
| x2 |
| 16 |
| y2 |
| 9 |
| A、2 | B、2或18 | C、18 | D、16 |
设F是椭圆
+y2=1的一个焦点，则椭圆上与点F的距离等于长半轴长点的坐标是（ ）
| x2 |
| 4 |
| A、（0，±2） | ||||
| B、（0，±1） | ||||
C、（
| ||||
D、（0，±
|
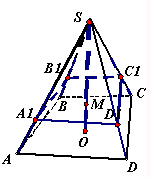如图，在四棱锥S-ABCD中，SO⊥平面ABCD，O为垂足，点M在SO上，且SM：MO=2：1，经过点M作与底面ABCD平行的平面α，分别交棱SA、SB、SC、SD于A1、B1、C1、D1
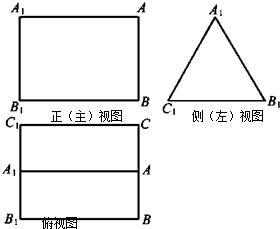如图是三棱柱ABC-A1B1C1的三视图，正（主）视图和俯视图都是矩形，侧（左）视图为等边三角形，D为AC的中点．