题目内容
若方程
+
=1表示的图形是双曲线，则k的取值范围为（ ）
| x2 |
| 2-k |
| y2 |
| k-1 |
| A、k＞2或k＜1 |
| B、1＜k＜2 |
| C、-2＜k＜1 |
| D、-1＜k＜2 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的标准方程，可得只需2-k与k-1只需异号即可，则可得不等式（2-k）（k-1）＜0，进而可得答案．
解答：
解：由题意知（2-k）（k-1）＜0，
解得k＜1或k＞2．
故选：A．
解得k＜1或k＞2．
故选：A．
点评：本题主要考查了双曲线的定义，属基础题；解答的关键是根据双曲线的标准方程建立不等关系．
练习册系列答案
阅读快车系列答案
相关题目
函数y=
x3-x的单调递减区间为（ ）
| 1 |
| 3 |
| A、[-1，1] |
| B、[0，1] |
| C、[1，+∞） |
| D、[0，+∞） |
已知2x+y=0是双曲线x2-λy2=1的一条渐近线，则双曲线的离心率是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、2 |
某人连续射击8次，命中4次且恰好有3次连在一起的结果有（ ）
| A、12种 | B、6种 |
| C、20种 | D、10种 |
以下公式中：①an=
[1-（-1）n]；②an=
；③an=
，可以作为数列
，0，
，0，
，0，…通项公式的是（ ）
| ||
| 2 |
| 1-(-1)n |
|
| 2 |
| 2 |
| 2 |
| A、①② | B、②③ | C、①③ | D、①②③ |
若p是q的逆否命题，S是q的否命题，则p是S的（ ）
| A、逆命题 | B、原命题 |
| C、否命题 | D、逆否命题 |
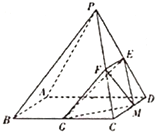如图，已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，E、F、G分别是PD、PC、BC的中点．