题目内容
已知函数f(x)=ax+xlnx,且图象在点(
,f(
))处的切线斜率为1(e为自然对数的底数).
(Ⅰ)求实数a的值;
(Ⅱ)设g(x)=
,求g(x)的单调区间.
| 1 |
| e |
| 1 |
| e |
(Ⅰ)求实数a的值;
(Ⅱ)设g(x)=
| f(x)-x |
| x-1 |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由f(x)=ax+xlnx,得f′(x)=a+1+lnx,依题意f′(
)=a=1,从而求出a=1.
(Ⅱ)由g′(x)=
,设h(x)=x-1-lnx,则h′(x)=1-
,讨论①当x>1时,②当0<x<1时的情况,得出g(x)的单调增区间为(0,1),(1,+∞).
| 1 |
| e |
(Ⅱ)由g′(x)=
| x-1-lnx |
| (x-1)2 |
| 1 |
| x |
解答:
解:(Ⅰ)f(x)=ax+xlnx,
∴f′(x)=a+1+lnx,
依题意f′(
)=a=1,
∴a=1.
(Ⅱ)∵g(x)=
,
∴g′(x)=
,
设h(x)=x-1-lnx,
则h′(x)=1-
,
当x>1时,h′(x)>0,h(x)是增函数.
对?x>1,h(x)>h(1)=0,即当x>1时,g′(x)>0,
故g(x)在(1,+∞)上为增函数,
当0<x<1时,h′(x)<0,h(x)是减增函数.
对?x∈(0,1),h(x)>h(1)=0,即当0<x<1时,g′(x)>0,
故g(x)在(0,1)上为增函数,
∴g(x)的单调增区间为(0,1),(1,+∞).
∴f′(x)=a+1+lnx,
依题意f′(
| 1 |
| e |
∴a=1.
(Ⅱ)∵g(x)=
| xlnx |
| x-1 |
∴g′(x)=
| x-1-lnx |
| (x-1)2 |
设h(x)=x-1-lnx,
则h′(x)=1-
| 1 |
| x |
当x>1时,h′(x)>0,h(x)是增函数.
对?x>1,h(x)>h(1)=0,即当x>1时,g′(x)>0,
故g(x)在(1,+∞)上为增函数,
当0<x<1时,h′(x)<0,h(x)是减增函数.
对?x∈(0,1),h(x)>h(1)=0,即当0<x<1时,g′(x)>0,
故g(x)在(0,1)上为增函数,
∴g(x)的单调增区间为(0,1),(1,+∞).
点评:本题考察了函数的单调性,导数的应用,求参数的值,渗透了分类讨论思想,是一道综合题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
已知2x+y=0是双曲线x2-λy2=1的一条渐近线,则双曲线的离心率是( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
若p是q的逆否命题,S是q的否命题,则p是S的( )
| A、逆命题 | B、原命题 |
| C、否命题 | D、逆否命题 |
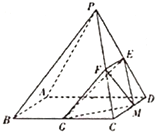 如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,E、F、G分别是PD、PC、BC的中点.