题目内容
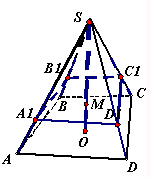如图，在四棱锥S-ABCD中，SO⊥平面ABCD，O为垂足，点M在SO上，且SM：MO=2：1，经过点M作与底面ABCD平行的平面α，分别交棱SA、SB、SC、SD于A1、B1、C1、D1（1）求证：四边形A1B1C1D1∽四边形ABCD；
（2）求棱锥S-A1B1C1D1的体积与棱台A1B1C1D1-ABCD的体积之比．
考点：棱柱、棱锥、棱台的体积,棱锥的结构特征
专题：计算题,空间位置关系与距离
分析：（1）用面面平行的性质定理；
（2）用小锥与大锥体积比等于相似比的立方比进行转化．
（2）用小锥与大锥体积比等于相似比的立方比进行转化．
解答：
（1）证明：∵SM：MO=2：1，经过点M作与底面ABCD平行的平面α，
∴A1B1∥AB，B1C1∥BC，C1D1∥CD，DA∥DA，
∴四边形A1B1C1D1∽四边形ABCD，相似比为2：3；
（2）解：∵相似比为2：3，
∴VS-A1B1C1D1：VS-ABCD=8：27，
∴棱锥S-A1B1C1D1的体积与棱台A1B1C1D1-ABCD的体积之比为8：19．
∴A1B1∥AB，B1C1∥BC，C1D1∥CD，DA∥DA，
∴四边形A1B1C1D1∽四边形ABCD，相似比为2：3；
（2）解：∵相似比为2：3，
∴VS-A1B1C1D1：VS-ABCD=8：27，
∴棱锥S-A1B1C1D1的体积与棱台A1B1C1D1-ABCD的体积之比为8：19．
点评：本题考查面面平行的性质定理，考查体积的计算，属于中档题．
练习册系列答案
相关题目
设f（x）=x2（2-x），则f（x）的单调增区间是（ ）
A、x∈（0，
| ||
B、x∈（
| ||
| C、x∈（-∞，0） | ||
D、x∈（-∞，0）∪（
|
以下公式中：①an=
[1-（-1）n]；②an=
；③an=
，可以作为数列
，0，
，0，
，0，…通项公式的是（ ）
| ||
| 2 |
| 1-(-1)n |
|
| 2 |
| 2 |
| 2 |
| A、①② | B、②③ | C、①③ | D、①②③ |
若p是q的逆否命题，S是q的否命题，则p是S的（ ）
| A、逆命题 | B、原命题 |
| C、否命题 | D、逆否命题 |
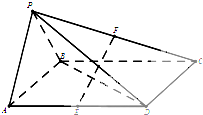四棱锥P-ABCD底面是平行四边形，面PAB⊥面ABCD，PA=PB=AB=