题目内容
19.若空间中四个不重合的平面a1,a2,a3,a4满足a1⊥a2,a2⊥a3,a3⊥a4,则下列结论一定正确的是( )| A. | a1⊥a4 | B. | a1∥a4 | ||
| C. | a1与a4既不垂直也不平行 | D. | a1与a4的位置关系不确定 |
分析 可得平面a1,a3平行或相交,而a3⊥a4,可得a1与a4的位置关系不确定,
解答 解:∵若空间中四个不重合的平面a1,a2,a3,a4满足a1⊥a2,a2⊥a3,a3⊥a4,
∴平面a1,a3平行或相交,∵a3⊥a4,∴a1与a4的位置关系不确定,
故选D.
点评 本题考查平面与平面位置关系的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
9.已知集合A={x|2+x-x2>0},B={x∈N|-2<x<5},则A∩B=( )
| A. | {0,1} | B. | {3,4} | C. | (-1,2) | D. | ∅ |
14.已知集合M={x|$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1},N={y|$\frac{x}{3}$+$\frac{y}{2}$=1},M∩N=( )
| A. | ∅ | B. | {(3,0),(0,2)} | C. | [一2,2] | D. | [一3,3] |
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且其图象向右平移$\frac{π}{6}$个单位后得到函数g(x)=sinωx的图象,则φ等于( )
| A. | -$\frac{π}{3}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
11.某宣传部门网站为弘扬社会主义思想文化,开展了以核心价值观为主题的系列宣传活动,并以“社会主义核心价值观”作为关键词便于网民搜索.此后,该网站的点击量每月都比上月增长50%,那么4个月后,该网站的点击量和原来相比,增长为原来的( )
| A. | 2倍以上,但不超过3倍 | B. | 3倍以上,但不超过4倍 | ||
| C. | 4倍以上,但不超过5倍 | D. | 5倍以上,但不超过6倍 |
8.不等式组$\left\{\begin{array}{l}x≥2\\ x+y≥6\\ x-2y≤0\end{array}\right.$所表示的平面区域为Ω,若直线ax-y+a+1=0与Ω有公共点,则实数a的最小值为( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 1 |
9.设函数$f(x)=sin({x+\frac{π}{4}})+cos({x-\frac{π}{4}})$,则( )
| A. | $f(x)=-f({x+\frac{π}{2}})$ | B. | $f(x)=f({-x+\frac{π}{2}})$ | C. | $f(x)•f({x+\frac{π}{2}})=1$ | D. | $f(x)=-f({-x+\frac{π}{2}})$ |
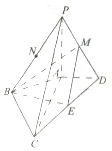 在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD,PA=AC=2AD=4,AB=BC=2$\sqrt{5}$,M,N,E分别为PD,PB,CD的中点.