题目内容
8.不等式组$\left\{\begin{array}{l}x≥2\\ x+y≥6\\ x-2y≤0\end{array}\right.$所表示的平面区域为Ω,若直线ax-y+a+1=0与Ω有公共点,则实数a的最小值为( )| A. | $-\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | 1 |
分析 由约束条件作出可行域,再由直线ax-y+a+1=0恒过定点,数形结合得答案.
解答 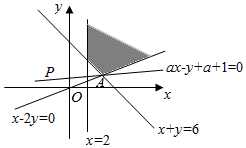 解:由约束条件$\left\{\begin{array}{l}x≥2\\ x+y≥6\\ x-2y≤0\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}x≥2\\ x+y≥6\\ x-2y≤0\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x-2y=0}\\{x+y=6}\end{array}\right.$,解得A(4,2),
而直线ax-y+a+1=0恒过定点P(-1,1),
∵${k}_{PA}=\frac{2-1}{4-(-1)}=\frac{1}{5}$.
∴使直线ax-y+a+1=0与Ω有公共点的实数a的最小值为$\frac{1}{5}$.
故选:B.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.若空间中四个不重合的平面a1,a2,a3,a4满足a1⊥a2,a2⊥a3,a3⊥a4,则下列结论一定正确的是( )
| A. | a1⊥a4 | B. | a1∥a4 | ||
| C. | a1与a4既不垂直也不平行 | D. | a1与a4的位置关系不确定 |
3.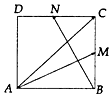 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
 如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )
如图,在正方形ABCD中,M,N分别是BC,CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λ+μ的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | 1 | D. | -1 |
13.已知等比数列{an},且a6+a8=$\int_0^4{\sqrt{16-{x^2}}dx}$,则a8(a4+2a6+a8)的值为( )
| A. | π2 | B. | 4π2 | C. | 8π2 | D. | 16π2 |
 如图,在直三棱柱ABC-A1B1C1中,底面△ABC是等腰直角三角形,且斜边AB=$\sqrt{2}$,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).
如图,在直三棱柱ABC-A1B1C1中,底面△ABC是等腰直角三角形,且斜边AB=$\sqrt{2}$,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).