题目内容
已知平面α，命题甲：若a∥α，b∥α，则a∥b，命题乙：若a⊥α，b⊥α，则a∥b，则下列说法正确的是（ ）
| A、当a，b均为直线时，命题甲、乙都是真命题 |
| B、当a，b均为平面时，命题甲、乙都是真命题 |
| C、当a为直线，b为平面时，命题甲、乙都是真命题 |
| D、当a为平面，b为直线时，命题甲、乙都是假命题 |
考点：空间中直线与平面之间的位置关系
专题：开放型,空间位置关系与距离
分析：根据线面平行、垂直的性质与判定，进行判断，即可得出结论．
解答：
解：对于A，当a，b均为直线时，命题甲是假命题、乙是真命题，故不正确；
对于B，当a，b均为平面时，命题甲是真命题、乙是假命题，故不正确；
对于C，当a为直线，b为平面时，命题甲、乙都是假命题，故不正确；
对于D，当a为平面，b为直线时，命题甲、乙都是假命题，正确．
故选：D．
对于B，当a，b均为平面时，命题甲是真命题、乙是假命题，故不正确；
对于C，当a为直线，b为平面时，命题甲、乙都是假命题，故不正确；
对于D，当a为平面，b为直线时，命题甲、乙都是假命题，正确．
故选：D．
点评：本题主要考查对空间点、线、面位置关系的概念、定理的理解和应用，属于中档题．
练习册系列答案
考前必练系列答案
相关题目
下列各组命题：
（1）p：a+b=2，q：直线x+y=0与圆（x-a）2+（y-b）2=2相切；
（2）p：|x|=x，q：x2+x≥0；
（3）设l，m均为直线，σ为平面，其中l?σ，m⊆σ，p：l∥σ，q：l∥m．
（4）p：数列log3n，log3（n+1），log3（n+3），（n∈N*）成等差数列；q：数列(
)n，
，3n（n∈N*）成等比数列．
其中，p是q的充分不必要条件的是（ ）
（1）p：a+b=2，q：直线x+y=0与圆（x-a）2+（y-b）2=2相切；
（2）p：|x|=x，q：x2+x≥0；
（3）设l，m均为直线，σ为平面，其中l?σ，m⊆σ，p：l∥σ，q：l∥m．
（4）p：数列log3n，log3（n+1），log3（n+3），（n∈N*）成等差数列；q：数列(
| 1 |
| 3 |
| 3 |
| 3n |
其中，p是q的充分不必要条件的是（ ）
| A、（1）（2） |
| B、（1）（4） |
| C、（1）（3） |
| D、（2）（3）（4） |
若a=(
)2，b=x
，c=log
x，则当x＞1时，a，b，c的大小关系是（ ）
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| A、a＜b＜c |
| B、c＜b＜a |
| C、c＜a＜b |
| D、a＜c＜b |
已知实数x∈[1，10]，执行如图所示的程序框图，则输出x的值不小于55的概率为（ ）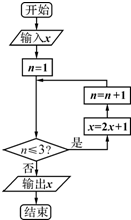
A、
| ||
B、
| ||
C、
| ||
D、
|
下列判断正确的是（ ）
| A、“正四棱锥的底面是正方形”的逆命题为真命题． | ||
| B、“ac2＞bc2”的充要条件是“a＞b”． | ||
C、不等式
| ||
| D、若“p或q”是真命题，则p，q中至少有一个真命题． |
若函数f（x）=（x+1）（x-a）是偶函数，则实数a的值为（ ）
| A、1 | B、0 | C、-1 | D、±1 |