题目内容
数列{an}的前n项和为Sn,若a1=1,an+1=3Sn(n≥1),则a6= .
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由数列递推式求得a2,在数列递推式中取n=n-1得另一递推式,作差后得到数列除去第一项后,为首项是3,公比为4的等比数列,写出n≥2时的通项公式后即可求得a6的值.
解答:
解:由an+1=3Sn,得到an=3Sn-1(n≥2),
两式相减得:an+1-an=3(Sn-Sn-1)=3an,
则an+1=4an(n≥2),又a1=1,a2=3S1=3a1=3,
得到此数列除去第一项后,为首项是3,公比为4的等比数列,
∴an=a2qn-2=3×4n-2(n≥2).
则a6=3×44=768.
故答案为:768.
两式相减得:an+1-an=3(Sn-Sn-1)=3an,
则an+1=4an(n≥2),又a1=1,a2=3S1=3a1=3,
得到此数列除去第一项后,为首项是3,公比为4的等比数列,
∴an=a2qn-2=3×4n-2(n≥2).
则a6=3×44=768.
故答案为:768.
点评:本题考查了数列递推式,考查了等比关系的确定,关键是明确从第二项起数列为等比数列,是中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
若z=
=x+yi,x,y∈R,则集合{x,2x,y}子集个数是( )
| 2-i |
| 1+2i |
| A、8 | B、7 | C、6 | D、9 |
已知平面α,命题甲:若a∥α,b∥α,则a∥b,命题乙:若a⊥α,b⊥α,则a∥b,则下列说法正确的是( )
| A、当a,b均为直线时,命题甲、乙都是真命题 |
| B、当a,b均为平面时,命题甲、乙都是真命题 |
| C、当a为直线,b为平面时,命题甲、乙都是真命题 |
| D、当a为平面,b为直线时,命题甲、乙都是假命题 |
设变量x,y满足约束条件
,则目标函数z=3x-y的最小值为( )
|
| A、-8 | B、-6 | C、-4 | D、-2 |

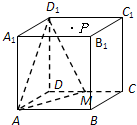 如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为
如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为