题目内容
下列各组命题:
(1)p:a+b=2,q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,σ为平面,其中l?σ,m⊆σ,p:l∥σ,q:l∥m.
(4)p:数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列;q:数列(
)n,
,3n(n∈N*)成等比数列.
其中,p是q的充分不必要条件的是( )
(1)p:a+b=2,q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,σ为平面,其中l?σ,m⊆σ,p:l∥σ,q:l∥m.
(4)p:数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列;q:数列(
| 1 |
| 3 |
| 3 |
| 3n |
其中,p是q的充分不必要条件的是( )
| A、(1)(2) |
| B、(1)(4) |
| C、(1)(3) |
| D、(2)(3)(4) |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:利用充分条件和必要条件的对应分别进行判断即可得到结论.
解答:
解:(1)若直线x+y=0与圆(x-a)2+(y-b)2=2相切,则圆心到直线的距离d=
=
,即|a+b|=2,
∴p是q的充分不必要条件.
(2)由|x|=x得x≥0,由x2+x≥0得x≥0或x≤-1,∴p是q的充分不必要条件.
(3)根据线面平行的判定定理可知p是q的必要不充分条件.
(4)若数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列,
则log3n+log3(n+3)=2log3(n+1),
即n(n+3)=(n+1)2,∴3n=2n+1,即n=1,
若数列(
)n,
,3n(n∈N*)成等比数列,
则(
)n•3n=(
)2=1,解得n=1,
∴p是q的充分必要条件,
故选:A.
| |a+b| | ||
|
| 2 |
∴p是q的充分不必要条件.
(2)由|x|=x得x≥0,由x2+x≥0得x≥0或x≤-1,∴p是q的充分不必要条件.
(3)根据线面平行的判定定理可知p是q的必要不充分条件.
(4)若数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列,
则log3n+log3(n+3)=2log3(n+1),
即n(n+3)=(n+1)2,∴3n=2n+1,即n=1,
若数列(
| 1 |
| 3 |
| 3 |
| 3n |
则(
| 1 |
| 3 |
| 3 |
| 3n |
∴p是q的充分必要条件,
故选:A.
点评:本题主要考查充分条件和必要条件的判断和应用,涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
若z=
=x+yi,x,y∈R,则集合{x,2x,y}子集个数是( )
| 2-i |
| 1+2i |
| A、8 | B、7 | C、6 | D、9 |
函数f(x)=sin(ωx+φ)cos(ωx+φ)(ω>0)的相邻的两个对称中心的距离为1,且能在x=2时取得最大值,则φ的一个值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知平面α,命题甲:若a∥α,b∥α,则a∥b,命题乙:若a⊥α,b⊥α,则a∥b,则下列说法正确的是( )
| A、当a,b均为直线时,命题甲、乙都是真命题 |
| B、当a,b均为平面时,命题甲、乙都是真命题 |
| C、当a为直线,b为平面时,命题甲、乙都是真命题 |
| D、当a为平面,b为直线时,命题甲、乙都是假命题 |
 一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )
一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )| A、42cm3 |
| B、48cm3 |
| C、56cm3 |
| D、44cm3 |

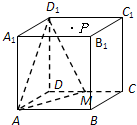 如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为
如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为