题目内容
已知实数x∈[1,10],执行如图所示的程序框图,则输出x的值不小于55的概率为( )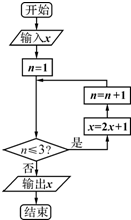

A、
| ||
B、
| ||
C、
| ||
D、
|
考点:程序框图
专题:概率与统计,算法和程序框图
分析:由程序框图的流程,写出前三项循环得到的结果,得到输出的值与输入的值的关系,令输出值大于等于54得到输入值的范围,利用几何概型的概率公式求出输出的x不小于55的概率.
解答:
解:设实数x∈[0,10],
经过第一次循环得到x=2x+1,n=2
经过第二循环得到x=2(2x+1)+1,n=3
经过第三次循环得到x=2[2(2x+1)+1]+1,n=4此时输出x
输出的值为8x+7
令8x+7≥55,得x≥6
由几何概型得到输出的x不小于55的概率为=
=
.
故选:C
经过第一次循环得到x=2x+1,n=2
经过第二循环得到x=2(2x+1)+1,n=3
经过第三次循环得到x=2[2(2x+1)+1]+1,n=4此时输出x
输出的值为8x+7
令8x+7≥55,得x≥6
由几何概型得到输出的x不小于55的概率为=
| 10-6 |
| 10-1 |
| 4 |
| 9 |
故选:C
点评:根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型⇒③解模.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
函数f(x)=sin(ωx+φ)cos(ωx+φ)(ω>0)的相邻的两个对称中心的距离为1,且能在x=2时取得最大值,则φ的一个值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知平面α,命题甲:若a∥α,b∥α,则a∥b,命题乙:若a⊥α,b⊥α,则a∥b,则下列说法正确的是( )
| A、当a,b均为直线时,命题甲、乙都是真命题 |
| B、当a,b均为平面时,命题甲、乙都是真命题 |
| C、当a为直线,b为平面时,命题甲、乙都是真命题 |
| D、当a为平面,b为直线时,命题甲、乙都是假命题 |
设双曲线
-
=1(a>0)的渐近线方程为3x±2y=0,则
(
)dx的值为( )
| x2 |
| a2 |
| y2 |
| 9 |
| ∫ | a 1 |
| 1 |
| x |
| A、ln2 | B、0 | C、ln3 | D、1 |
 一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )
一个简单组合体的三视图及尺寸如图所示(单位:cm),该组合体的体积为( )| A、42cm3 |
| B、48cm3 |
| C、56cm3 |
| D、44cm3 |
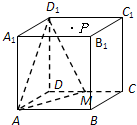 如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为
如图,正方体ABCD-A1B1C1D1的棱长为2,P是底面A1B1C1D1的中心,M是CD的中点,则P到平面AMD1的距离为