题目内容
已知f(x)为定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数解析式为f(x)=
-
(b∈R)
(Ⅰ)求b的值,并求出f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
| 1 |
| 4x |
| b |
| 2x |
(Ⅰ)求b的值,并求出f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(Ⅰ)利用奇函数f(0)=0,即可求出b的值,利用函数的奇偶性直接并求出f(x)在[0,1]上的解析式;
(Ⅱ)利用换元法化简函数为求f(x)为二次函数,然后求解在[0,1]上的最值.
(Ⅱ)利用换元法化简函数为求f(x)为二次函数,然后求解在[0,1]上的最值.
解答:
解:(Ⅰ)∵f(x)为定义在[-1,1]上的奇函数,且f(x)在x=0处有意义,
∴f(0)=0,即f(0)═1-b=0.b=1…(3分)
设x∈[0,1],则-x∈[-1,0].
∴f(-x)=
-
=4x-2x.
又∵f(-x)=-f(x)
∴-f(x)=4x-2x.
∴f(x)=2x-4x.
所以,f(x)在[0,1][上的解析式为f(x)=2x-4x…(6分)
(Ⅱ)当x∈[0,1],f(x)=2x-4x=2x-(2x)2,
∴设t=2x(t>0),则f(t)=t-t2.
∵x∈[0,1],∴t∈[1,2].
当t=1时,取最大值,最大值为1-1=0.
当t=0时,取最小值为-2.
所以,函数在[0,1]上的最大与最小值分别为0,-2…(12分)
∴f(0)=0,即f(0)═1-b=0.b=1…(3分)
设x∈[0,1],则-x∈[-1,0].
∴f(-x)=
| 1 |
| 4-x |
| 1 |
| 2-x |
又∵f(-x)=-f(x)
∴-f(x)=4x-2x.
∴f(x)=2x-4x.
所以,f(x)在[0,1][上的解析式为f(x)=2x-4x…(6分)
(Ⅱ)当x∈[0,1],f(x)=2x-4x=2x-(2x)2,
∴设t=2x(t>0),则f(t)=t-t2.
∵x∈[0,1],∴t∈[1,2].
当t=1时,取最大值,最大值为1-1=0.
当t=0时,取最小值为-2.
所以,函数在[0,1]上的最大与最小值分别为0,-2…(12分)
点评:本题考查换元法的应用,函数的奇偶性以及函数的解析式的求法二次函数的闭区间上的最值的求法,考查计算能力.

练习册系列答案
相关题目
若函数f(x)=|4x-x2|+2a-8至少有3个零点,则实数a的取值范围是( )
| A、(-∞,3) |
| B、(-∞,3] |
| C、[2,3) |
| D、[2,3] |
在△ABC中,已知6
•
=2
•
=3
•
,则∠A=( )
| AC |
| AB |
| AB |
| BC |
| BC |
| CA |
| A、30° | B、45° |
| C、120° | D、135° |
已知ω>0,函数f(x)=sin(ωx+
)在(
,π)上单调递减,则ω的取值范围是( )
| π |
| 6 |
| π |
| 2 |
A、[
| ||||
B、[
| ||||
C、(0,
| ||||
D、(0,
|
已知回归直线的斜率的估计值为1.4,样本点的中心为(5,9),则回归直线方程为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
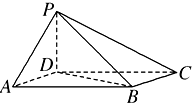 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.