题目内容
已知ω＞0，函数f(x)=sin(ωx+
)在(
，π)上单调递减，则ω的取值范围是（ ）
| π |
| 6 |
| π |
| 2 |
A、[
| ||||
B、[
| ||||
C、(0，
| ||||
D、(0，
|
考点：y=Asin（ωx+φ）中参数的物理意义
专题：三角函数的图像与性质
分析：结合特殊值，求解三角函数的递减区间，并验证结果即可．
解答：
解：取ω=
，f(x)=sin(
x+
)，其减区间为[
+
，
+π]（k∈Z），
显然(
，π)⊆[
+
，
+π]（k∈Z），
∵0＜
＜
＜
，即[
，
]，(0，
]不在减区间内．
∴排除B，C；
取ω=
，f(x)=sin(
x+
)，其减区间为[
+
，
+
]（k∈Z），
显然(
，π)?[
+
，
+
]（k∈Z），
∵0＜
＜
，即(0，
]不在减区间内．
∴排除D．
故选：A．
| 4 |
| 3 |
| 4 |
| 3 |
| π |
| 6 |
| 3kπ |
| 2 |
| π |
| 4 |
| 3kπ |
| 2 |
显然(
| π |
| 2 |
| 3kπ |
| 2 |
| π |
| 4 |
| 3kπ |
| 2 |
∵0＜
| 2 |
| 3 |
| 3 |
| 4 |
| π |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
∴排除B，C；
取ω=
| 3 |
| 2 |
| 3 |
| 2 |
| π |
| 6 |
| 4kπ |
| 3 |
| 2π |
| 9 |
| 4kπ |
| 3 |
| 8π |
| 9 |
显然(
| π |
| 2 |
| 4kπ |
| 3 |
| 2π |
| 9 |
| 4kπ |
| 3 |
| 8π |
| 9 |
∵0＜
| 3 |
| 2 |
| π |
| 2 |
| 3 |
| 2 |
∴排除D．
故选：A．
点评：本题主要考察了三角函数的图象与性质，属于基本知识的考查．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
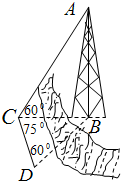测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D．现测得∠BCD=75°，∠BDC=60°，CD=100m．并在点C测得塔顶A的仰角∠ACB=60°，求：塔高AB．
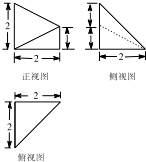某几何体的三视图如图所示，该几何体的表面积是对任意的正数s，t，有下列4个关系式：
①f（s+t）=f（s）+f（t）；
②f（s+t）=f（s）f（t）；
③f（st）=f（s）+f（t）；
④f（st）=f（s）f（t）．
则下列函数中，不满足任何一个关系式的是（ ）
①f（s+t）=f（s）+f（t）；
②f（s+t）=f（s）f（t）；
③f（st）=f（s）+f（t）；
④f（st）=f（s）f（t）．
则下列函数中，不满足任何一个关系式的是（ ）
| A、y=kx+b（kb≠0） |
| B、y=x2 |
| C、y=ax（a＞0，且a≠1） |
| D、y=logax（a＞0，且a≠1） |