题目内容
已知F是定点,l为定直线,点F到l的距离为p(p>0),点M在直线l上移动,动点N在MF的延长线上,且满足|FN|•|MF|=|MN|,求动点N的轨迹方程.
考点:与直线有关的动点轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:过F作FA⊥l于A,分别以AF,l为x,y轴建立直角坐标系,设出N的坐标,结合已知|FN|•|MF|=|MN|列等式,再由三角形相似列比例式,整理后即可得到动点N的轨迹方程.
解答:
解:如图,
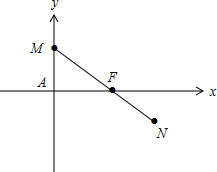
作FA⊥l于A,分别以AF,l为x,y轴建立直角坐标系,则F(p,0),
设N(x,y),x>p,M(0,m),则
=-
,m=-
,①
由|FN|•|MF|=|MN|,得|FN|:|MN|=1:|MF|,
则(x-p):x=1:
,
平方得
=p2+m2,②
把①代入②,得
=p2+
,
∴x2-p2y2=p2(x-p)2,
∴(p2-1)x2+p2y2-2p3x+p4=0,x>p≥1,即为动点N的轨迹方程.

作FA⊥l于A,分别以AF,l为x,y轴建立直角坐标系,则F(p,0),
设N(x,y),x>p,M(0,m),则
| y |
| x-p |
| m |
| p |
| py |
| x-p |
由|FN|•|MF|=|MN|,得|FN|:|MN|=1:|MF|,
则(x-p):x=1:
| p2+m2 |
平方得
| x2 |
| (x-p)2 |
把①代入②,得
| x2 |
| (x-p)2 |
| p2y2 |
| (x-p)2 |
∴x2-p2y2=p2(x-p)2,
∴(p2-1)x2+p2y2-2p3x+p4=0,x>p≥1,即为动点N的轨迹方程.
点评:本题考查了轨迹方程的求法,解答此题的关键是由题意列出比例式,结合已知等式找N的关系式,是中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知数列{an}的通项公式an=
,Sn为其前n项和,则S6=( )
| 2n-1 |
| 2n |
A、
| ||
B、
| ||
C、
| ||
D、
|
 设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )
设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )




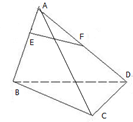 如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.
如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.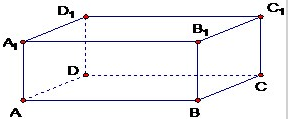 长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).
长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).