题目内容
设函数f（x）在定义域内可导，y=f（x）的图象如图所示，则导函数y=f′（x）可能为（ ）A、 |
B、 |
C、 |
D、 |
考点：函数的图象,导数的运算
专题：函数的性质及应用
分析：先从f（x）的图象判断出f（x）的单调性，根据函数的单调性与导函数的符号的关系判断出导函数的符号，判断出导函数的图象
解答：
解：由f（x）的图象判断出
f（x）在区间（-∞，0）上递增；在（0，+∞）上先增再减再增
∴在区间（-∞，0）上f′（x）＞0，在（0，+∞）上先有f′（x）＞0再有f′（x）＜0再有f′（x）＞0
故选D．
f（x）在区间（-∞，0）上递增；在（0，+∞）上先增再减再增
∴在区间（-∞，0）上f′（x）＞0，在（0，+∞）上先有f′（x）＞0再有f′（x）＜0再有f′（x）＞0
故选D．
点评：本题主要考查函数的单调性与其导函数的正负之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减，属于基础题
练习册系列答案
相关题目
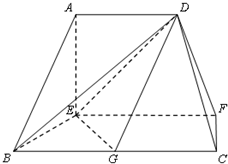在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF∥BC，BC=2AD=4，AE=BE=2，G是BC的中点．