题目内容
设过点P(2,1)的直线l与x轴、y轴的正半轴分别交于点A、B,O为坐标原点,且△AOB的面积>
,求直线l的斜率k的取值范围.
| 9 |
| 2 |
考点:直线的点斜式方程
专题:直线与圆
分析:先设直线的斜率为k,得到直线方程,分别求出OA,OB的长,再表示出面积,得到关于k的不等式,解得即可.
解答:
解:设直线的斜率为k,因为直线与x轴y轴正半轴分别相交,所以k<0,
因为经过点P(2,1),则直线I的方程为y-1=k(x-2)整理得:kx-y+1-2k=0,
当x=0时,y=|OB|=1-2k>0,当y=0时,x=|OA|=2-
>0,
所以S△AOB=
|0B||0A|=
(1-2k)(2-
)
因为△AOB的面积大于
,
所以
(1-2k)(2-
)>9,
∴4k2+14k+1>0,
解得k<
,或
<k<0,
故直线l的斜率k的取值范围(-∞,
)∪(
,0),
因为经过点P(2,1),则直线I的方程为y-1=k(x-2)整理得:kx-y+1-2k=0,
当x=0时,y=|OB|=1-2k>0,当y=0时,x=|OA|=2-
| 1 |
| k |
所以S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| k |
因为△AOB的面积大于
| 9 |
| 2 |
所以
| 1 |
| 2 |
| 1 |
| k |
∴4k2+14k+1>0,
解得k<
-7-3
| ||
| 4 |
-7+3
| ||
| 4 |
故直线l的斜率k的取值范围(-∞,
-7-3
| ||
| 4 |
-7+3
| ||
| 4 |
点评:本题主要考查了直线方程和,基本不等式的解法,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
若实数x,y满足
,则x2+y2的最小值是( )
|
A、
| ||||
| B、5 | ||||
C、
| ||||
D、
|
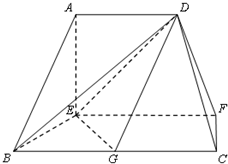 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4,AE=BE=2,G是BC的中点.