Question

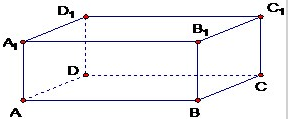长方体ABCD-A₁B₁C₁D₁中，AB=2，BC=1，AA₁=1（利用空间向量求解及证明）．
（1）求直线AD₁与B₁D所成角；
（2）证明：BD₁⊥B₁C．

Answer 1

考点：异面直线及其所成的角

专题：计算题,证明题,空间位置关系与距离,空间角

分析：（1）以B为坐标原点，BA，BC，BB₁为x，y，z轴，建立空间直角坐标系，求出A（2，0，0），D₁（2，1，1），D（2，1，0），B₁（0，0，1），得到向量AD₁与B₁D的坐标，再由夹角公式，即可得到；
（2）求得D₁（2，1，1），B（0，0，0），B₁（0，0，1），C（0，1，0），再求向量BD₁，B₁C的坐标，再求出向量的数量积，即可得证．

解答： （1）解：以B为坐标原点，BA，BC，BB₁为x，y，z轴
建立空间直角坐标系，
则A（2，0，0），D₁（2，1，1），D（2，1，0），
B₁（0，0，1），

AD1

=（0，1，1），

B1D

=（2，1，-1），
则cos＜

AD1

，

B1D

＞=

AD1 • B1D

| AD1 |•| B1D |

=

1×1-1×1

2 • 4+2

=0，则直线AD₁与B₁D所成角为90°；
（2）证明：由（1）得D₁（2，1，1），B（0，0，0），
B₁（0，0，1），C（0，1，0），
则

BD1

=（2，1，1），

B1C

=（0，1，-1），

BD1

•

B1C

=2×0+1×1+1×（-1）=0，
则BD₁⊥B₁C．

点评：本题考查空间异面直线所成的角以及线线位置关系，考查向量法解决空间角和线面位置关系，属于基础题．