题目内容
已知数列{an}的通项公式an=
,Sn为其前n项和,则S6=( )
| 2n-1 |
| 2n |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:先化简an=
=1-
,再列出S6,根据等比数列的求和公式计算即可.
| 2n-1 |
| 2n |
| 1 |
| 2n |
解答:
解:an=
=1-
,
∴S6=a1+a2+a3+a4+a5+a6=1-
+1-
+1-
+1-
+1-
+1-
=6-
=
,
故选:D
| 2n-1 |
| 2n |
| 1 |
| 2n |
∴S6=a1+a2+a3+a4+a5+a6=1-
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 25 |
| 1 |
| 26 |
| ||||
1-
|
| 321 |
| 64 |
故选:D
点评:本题主要考查了等比数列的求和公式,属于基础题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
在△ABC中,设
=
,
=
,
=
.若表示
、
、
的有向线段首尾相连能构成三角形,则△ABC的形状是( )
| a |
2
| ||
|
|
| b |
3
| ||
|
|
| c |
4
| ||
|
|
| a |
| b |
| c |
| A、等腰三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
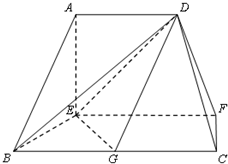 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4,AE=BE=2,G是BC的中点.