题目内容

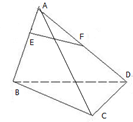如图，空间四边形ABCD中，E为AB的三等分点，即AB=3AE，F为AD的中点，求证：直线EF与平面BCD相交．
考点：空间中直线与平面之间的位置关系
专题：证明题,空间位置关系与距离
分析：由于AB=3AE，AF=FD，则EF与BD相交，延长EF，BD交于H，只要证得直线EF和平面BCD有且只有一个交点，即可．
解答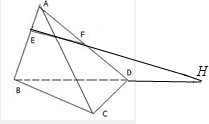： 证明：由于AB=3AE，AF=FD，
则EF与BD相交，延长EF，BD交于H，
则H在平面BCD内，
即有直线EF与平面BCD有一个交点H，
若还有一个交点在平面BCD内，
则由公理1，可得直线EF在平面BCD内，
这与E、F不在平面BCD内矛盾，
则直线EF和平面BCD有且只有一个交点，
即直线EF和平面BCD相交．
点评：本题考查空间直线与平面的位置关系，考查判断和推理能力，以及空间想象能力，属于基础题．
练习册系列答案
相关题目
下列命题中：
①函数f（x）=lg（x2+mx+m）的值域为R，则m∈（0，4）；
②若函数f（x）满足f（x+1）=
1+f(x)
1-f(x)
，则f（x）为周期函数；
③函数y=f（2-x）与y=f（2+x）的图象关于直线x=2对称；
④若函数f(x)=x+log2(x+
x2+1
)，则“m+n≥0”是“f（m）+f（n）≥0”的充要条件．
其中正确命题的序号是
 
．
已知F是定点，l为定直线，点F到l的距离为p（p＞0），点M在直线l上移动，动点N在MF的延长线上，且满足|FN|•|MF|=|MN|，求动点N的轨迹方程．
过点A（-1，-3），则斜率是直线y=3x的斜率的-
1
4
的直线方程
 
．
已知椭圆的中心在原点，一个焦点是（1，0），这个椭圆与直线y=x-1交于A、B两点，若以A、B为直径的圆过椭圆左焦点，求椭圆方程．
三棱锥P-ABC中，M、N、K分别是△PAB，△PBC，△PAC的重心，S△ABC=18．
（1）求证：MN
∥
.
1
3
AC；
（2）求S△MNK．
若实数x，y满足
x+y-3≥0
x-y-1≤0
y≤2
，则x2+y2的最小值是（　　）
A、
5
B、5
C、
3
2
2
D、
9
2
已知函数f（x）=
3
2
sin2x-
1+cos2x
2
-
1
2
，若x∈[
π
4
，
π
2
]，求函数f（x）的最值及对应x的值．
设变量x，y满足约束条件
x-y≥0
x+y≤4
y≥1
，则目标函数z=2x+y的最小值为（　　）
A、2B、3C、5D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网