题目内容
在平面直角坐标系xOy中,直线y=kx在矩阵
对应的变换下得到的直线过点P(4,1),求实数k的值.
|
考点:几种特殊的矩阵变换
专题:矩阵和变换
分析:设直线y=kx上任一点P(x,y)在矩阵
对应的变换下得到点P′(x′,y′),列出方程代入P坐标求解k即可.
|
解答:
解:设直线y=kx上任一点P(x,y)在矩阵
对应的变换下得到点P′(x′,y′)
则
=
,即
,即
(3分)
又点P(x,y)在直线y=kx上,所以x′=ky′,
把点(4,1)代入上式,得到4=k,
∴k=4(7分)
|
则
|
|
|
|
|
又点P(x,y)在直线y=kx上,所以x′=ky′,
把点(4,1)代入上式,得到4=k,
∴k=4(7分)
点评:本题考查矩阵与简单的变换,基本知识的考查.

练习册系列答案
相关题目
已知α∈(
,π),且sinα=
,则tanα=( )
| π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为( )
| A、x2+y2=32 |
| B、x2+y2=16 |
| C、(x-1)2+y2=16 |
| D、x2+(y-1)2=16 |
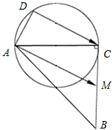 如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则
如图,已知:|AC|=|BC|=2,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则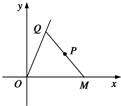 有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,