题目内容
已知焦点在y轴上的椭圆
+
=1的离心率为
,则m= .
| x2 |
| 9 |
| y2 |
| m+9 |
| 1 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据椭圆的方程表示焦点在y轴上的椭圆,得到a2=m+9,b2=9,从而得到c2=a2-b2=m.再利用离心率为
=
,建立关于m的等式,解之可得m的值.
| c |
| a |
| 1 |
| 2 |
解答:
解:∵椭圆
+
=1的焦点在y轴,
∴a2=m+9,b2=9,可得c2=a2-b2=m,
又∵椭圆的离心率等于
∴
=
⇒
=
=
∴m=3
故答案为:3.
| x2 |
| 9 |
| y2 |
| m+9 |
∴a2=m+9,b2=9,可得c2=a2-b2=m,
又∵椭圆的离心率等于
| 1 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
| c2 |
| a2 |
| m |
| m+9 |
| 1 |
| 4 |
∴m=3
故答案为:3.
点评:本题给出一个含有字母参数的方程,在已知离心率的情况下求参数m的值,考查了椭圆的基本概念,属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
p为椭圆
+
=1上的一点,F1,F2分别为左、右焦点,且∠F1PF2=60° 则|PF1|•|PF2|=( )
| x2 |
| 9 |
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
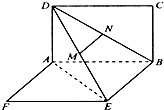 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为