题目内容
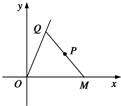 有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,(1)当P点平分线段MQ时,求直线MQ的方程;
(2)当△OMQ是以OM为底的等腰三角形时求出Q点坐标;
(3)点Q在什么位置时,△OMQ的面积最小,并求出最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设点M(m,0),则M点关于P点对称点为(12-m,8),由题可知,点(12-m,8)必在直线l上,由此能求出直线MQ方程.
(2)设点Q(x0,4x0),直线PQ的方程为y-4=
(x-6),由此能求出Q(
,14).
(3)设点Q(x0,4x0),则直线PQ的方程为y-4=
(x-6),点M的坐标为(
,0).设△OMQ的面积为S,则10x-Sx0+S=0,由此能求出点Q的坐标为(2,8)时,△OMQ的面积最小,且最小值为40.
(2)设点Q(x0,4x0),直线PQ的方程为y-4=
| 4x0-4 |
| x0-6 |
| 7 |
| 2 |
(3)设点Q(x0,4x0),则直线PQ的方程为y-4=
| 4x0-4 |
| x0-6 |
| 5x0 |
| x0-1 |
解答:
解:(1)设点M(m,0),则M点关于P点对称点为(12-m,8),
由题可知,点(12-m,8)必在直线l上,
∴8=4(12-m),即m=10,
∴M(10,0),直线MQ方程为2x+y-20=0.
(2)设点Q(x0,4x0),(x0>6,(x0≤6时不满足条件)),
∴直线PQ的方程为y-4=
(x-6).
令y=0得x=
,∴点M的坐标为(
,0),
由题可得|OQ|=|QM|,即x0=
,
∴Q(
,14)
(3)设点Q(x0,4x0)(x0>1且x0≠6),
则直线PQ的方程为y-4=
(x-6).
令y=0得x=
,∴点M的坐标为(
,0).
设△OMQ的面积为S,则S=
|OM|•4x0=,即10x-Sx0+S=0.
∴关于x0的一元二次方程有实根.
∴△=S2-40S≥0,即S≥40.
当S=40时,x0=2,4x0=8,∴点Q的坐标为(2,8).
而当x0=6时,点Q的坐标为(6,24),
此时S=
×6×24=72>40,不符合要求.
故当点Q的坐标为(2,8)时,△OMQ的面积最小,且最小值为40.
由题可知,点(12-m,8)必在直线l上,
∴8=4(12-m),即m=10,
∴M(10,0),直线MQ方程为2x+y-20=0.
(2)设点Q(x0,4x0),(x0>6,(x0≤6时不满足条件)),
∴直线PQ的方程为y-4=
| 4x0-4 |
| x0-6 |
令y=0得x=
| 5x0 |
| x0-1 |
| 5x0 |
| x0-1 |
由题可得|OQ|=|QM|,即x0=
| 7 |
| 2 |
∴Q(
| 7 |
| 2 |
(3)设点Q(x0,4x0)(x0>1且x0≠6),
则直线PQ的方程为y-4=
| 4x0-4 |
| x0-6 |
令y=0得x=
| 5x0 |
| x0-1 |
| 5x0 |
| x0-1 |
设△OMQ的面积为S,则S=
| 1 |
| 2 |
∴关于x0的一元二次方程有实根.
∴△=S2-40S≥0,即S≥40.
当S=40时,x0=2,4x0=8,∴点Q的坐标为(2,8).
而当x0=6时,点Q的坐标为(6,24),
此时S=
| 1 |
| 2 |
故当点Q的坐标为(2,8)时,△OMQ的面积最小,且最小值为40.
点评:本题考查直线MQ的方程的求法,考查Q点坐标的求法,考查点Q在什么位置时,△OMQ的面积最小,并求出最小值.解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
下列函数中,图象关于y轴对称的是( )
| A、y=log2x | ||
B、y=
| ||
| C、y=x|x| | ||
D、y=x -
|
 如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点,
如图,在正方体ABCD-A1B1C1D1中,E是AA1的中点,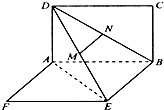 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为