题目内容
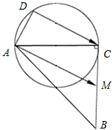如图，已知：|AC|=|BC|=2，∠ACB=90°，M为BC的中点，D为以AC为直径的圆上一动点，则| AM |
| DC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：建系可得
和
的坐标，进而可得
•
的表达式，由三角函数的值域可得．
| AM |
| DC |
| AM |
| DC |
解答：
解：建立如图所示的直角坐标系，则A（-1，0），C（1，0），），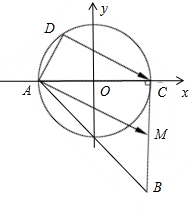
O（0，0），M（1，-1），设D（cosα，sinα）．
∴
=（2，-1），
=（1-cosα，-sinα）．
∴
•
=2（1-cosα）+sinα
=2+sinα-2cosα
=2+
sin（α-θ），其中tanθ=2．
∵sin（α-θ）∈[-1，1]，
∴2+
sin（α-θ）∈[2-
，2+
]，
∴
•
的取值范围是[2-
，2+
]
故答案为：[2-
，2+
]，
O（0，0），M（1，-1），设D（cosα，sinα）．
∴
| AM |
| DC |
∴
| AM |
| DC |
=2+sinα-2cosα
=2+
| 5 |
∵sin（α-θ）∈[-1，1]，
∴2+
| 5 |
| 5 |
| 5 |
∴
| AM |
| DC |
| 5 |
| 5 |
故答案为：[2-
| 5 |
| 5 |
点评：本题考查平面向量的数量积，涉及三角函数的值域，建系是解决问题的关键，属中档题．
练习册系列答案
相关题目
角α满足条件sinα•cosα＞0，sinα+cosα＜0，则α在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知-1，a，b，c，-4成等比数列，则实数b为（ ）
| A、4 | B、-2 | C、±2 | D、2 |
正方体AC1中，点P、Q分别为棱A1B1、DD1的中点，则PQ与AC1所成的角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |
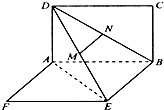如图，两矩形ABCD、ABEF所在平面互相垂直，DE与平面ABCD及平面ABEF所成角分别为30°、45°，M、N分别为DE与DB的中点，且MN=1，线段AB的长为