题目内容
甲、乙两人参加环保知识竞赛,共设有10个不同的题目,其中选择题6个,判断题4个.
(1)若甲、乙两人依次各抽一题,求甲抽到判断题,乙抽到选择题的概率是多少?
(2)若甲从中随机抽取5个题目,其中判断题的个数为ξ,求ξ的分布列和期望.
(1)若甲、乙两人依次各抽一题,求甲抽到判断题,乙抽到选择题的概率是多少?
(2)若甲从中随机抽取5个题目,其中判断题的个数为ξ,求ξ的分布列和期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)甲、乙两人依次各抽一题,由概率乘法公式能求出甲抽到判断题,乙抽到选择题的概率是.
(2)由已知得ξ的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和期望.
(2)由已知得ξ的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和期望.
解答:
解:(1)甲、乙两人依次各抽一题,
甲抽到判断题,乙抽到选择题的概率是:
p=
×
=
.
(2)由已知得ξ的可能取值为0,1,2,3,4,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
P(ξ=4)=
=
,
∴ξ的分布列为:
∴Eξ=0×
+1×
+2×
+3×
+4×
=2.
甲抽到判断题,乙抽到选择题的概率是:
p=
| 4 |
| 10 |
| 6 |
| 9 |
| 4 |
| 15 |
(2)由已知得ξ的可能取值为0,1,2,3,4,
P(ξ=0)=
| ||
|
| 6 |
| 252 |
P(ξ=1)=
| ||||
|
| 60 |
| 252 |
P(ξ=2)=
| ||||
|
| 120 |
| 254 |
P(ξ=3)=
| ||||
|
| 60 |
| 252 |
P(ξ=4)=
| ||||
|
| 6 |
| 252 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 6 |
| 252 |
| 60 |
| 252 |
| 120 |
| 252 |
| 60 |
| 252 |
| 6 |
| 252 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
p为椭圆
+
=1上的一点,F1,F2分别为左、右焦点,且∠F1PF2=60° 则|PF1|•|PF2|=( )
| x2 |
| 9 |
| y2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=log2
•log
(2x)的最小值为( )
| x |
| 2 |
| A、0 | ||
B、-
| ||
C、-
| ||
D、
|
下列函数中,图象关于y轴对称的是( )
| A、y=log2x | ||
B、y=
| ||
| C、y=x|x| | ||
D、y=x -
|
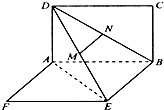 如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为
如图,两矩形ABCD、ABEF所在平面互相垂直,DE与平面ABCD及平面ABEF所成角分别为30°、45°,M、N分别为DE与DB的中点,且MN=1,线段AB的长为 在△ABC中,a,b,c分别是角A,B,C的对边,C=2A,cosA=
在△ABC中,a,b,c分别是角A,B,C的对边,C=2A,cosA=