题目内容
已知函数f(x)=2sinxcosx-1(x∈R),给出下列四个命题( )
①若f(x1)=-f(x2),则x1=-x2;
②f(x)的最小正周期是2π;
③f(x)在区间[-
,
]上是增函数;
④f(x)的图象关于直线x=
对称,
其中正确的命题是( )
①若f(x1)=-f(x2),则x1=-x2;
②f(x)的最小正周期是2π;
③f(x)在区间[-
| π |
| 4 |
| π |
| 4 |
④f(x)的图象关于直线x=
| 3π |
| 4 |
其中正确的命题是( )
| A、①②④ | B、①③ | C、②③ | D、③④ |
考点:二倍角的正弦
专题:三角函数的图像与性质
分析:f(x)=2sinxcosx-1=sin2x-1,
①若f(x1)=-f(x2)⇒sin2x1=sin2x2=1,不能推出x1=-x2,可判断①;
②利用正弦函数的周期公式可知f(x)的最小正周期是T=
=π≠2π,可判断②;
③由-
≤2x≤
得:-
≤x≤
,f(x)在区间[-
,
]上是增函数,可判断③;
④f(
)=sin
-1=-2,为其最小值,可判断④
①若f(x1)=-f(x2)⇒sin2x1=sin2x2=1,不能推出x1=-x2,可判断①;
②利用正弦函数的周期公式可知f(x)的最小正周期是T=
| 2π |
| 2 |
③由-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
④f(
| 3π |
| 4 |
| 3π |
| 2 |
解答:
解:∵函数f(x)=2sinxcosx-1=sin2x-1(x∈R),
①若f(x1)=-f(x2),则sin2x1-1+sin2x2-1=0,
所以,sin2x1+sin2x2=2,
所以,sin2x1=sin2x2=1,不能推出x1=-x2,故①错误;
②f(x)的最小正周期是T=
=π≠2π,故②错误;
③由-
≤2x≤
得:-
≤x≤
,f(x)在区间[-
,
]上是增函数,③正确;
④因为f(
)=sin
-1=-2,为其最小值,故f(x)的图象关于直线x=
对称,④正确.
其中正确的命题是③④,
故选:D.
①若f(x1)=-f(x2),则sin2x1-1+sin2x2-1=0,
所以,sin2x1+sin2x2=2,
所以,sin2x1=sin2x2=1,不能推出x1=-x2,故①错误;
②f(x)的最小正周期是T=
| 2π |
| 2 |
③由-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
④因为f(
| 3π |
| 4 |
| 3π |
| 2 |
| 3π |
| 4 |
其中正确的命题是③④,
故选:D.
点评:本题考查正弦函数的图象与性质,着重考查其周期性、单调性与对称轴的应用,属于中档题.

练习册系列答案
相关题目
已知f(x)=
-
,g(x)=|x-2|-2,记F(t)=
[f(x)-g(x)]dx,函数F(t)的导函数为F′(t),则函数y=F′(t),t∈(0,4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
| ∫ | t 0 |
A、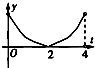 |
B、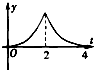 |
C、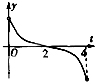 |
D、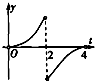 |
某商场经营的某种包装的大米质量服从正态分布N(10,0.12)(单位:kg),任选一袋这种大米,则质量在9.810.2kg的概率是( )
| A、0.9544 |
| B、0.9744 |
| C、0.6826 |
| D、0.5 |