题目内容
已知f(x)=
-
,g(x)=|x-2|-2,记F(t)=
[f(x)-g(x)]dx,函数F(t)的导函数为F′(t),则函数y=F′(t),t∈(0,4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
| ∫ | t 0 |
A、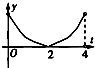 |
B、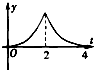 |
C、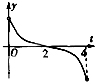 |
D、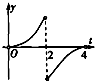 |
考点:函数的图象
专题:函数的性质及应用
分析:先化简两个函数的表达式,验证可知f(x)与g(x)均过(0,0)与(4,0),且在x∈(0,4)时f(x)的图象都在g(x)的上方,故在同一坐标系中画图,结合图象处理.
解答:
解:对于函数f(x)=
-
=
,此函数中的两段都可看成反比例函数经过平移得到,
且x≥2时不难验证图象过(2,
)与(4,0);而x≤2时不难验证图象过(2,
)与(0,0);
对于函数g(x)=|x-2|-2=
,此函数中的两段都可看成直线的一部分,
x≥2时不难验证图象过(2,-2)与(4,0);而x≤2时不难验证图象过(2,-2)与(0,0);
利用上述条件在同一个平面直角坐标系内画y=f(x)与y=g(x)图象:

又F(t)=
[f(x)-g(x)]dx表示由函数f(x)=
-
的图象、g(x)=|x-2|-2的图象与直线x=t围成的图形的面积,
∴从图象可以看出,t从0开始增大时,直线x=t向右移动,∵F(t)是增函数,且增的速度变化是先慢中间快再慢,
∴F′(t)的图象只有B符合.
故选:B.
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
|
且x≥2时不难验证图象过(2,
| 2 |
| 3 |
| 2 |
| 3 |
对于函数g(x)=|x-2|-2=
|
x≥2时不难验证图象过(2,-2)与(4,0);而x≤2时不难验证图象过(2,-2)与(0,0);
利用上述条件在同一个平面直角坐标系内画y=f(x)与y=g(x)图象:

又F(t)=
| ∫ | 1 0 |
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
∴从图象可以看出,t从0开始增大时,直线x=t向右移动,∵F(t)是增函数,且增的速度变化是先慢中间快再慢,
∴F′(t)的图象只有B符合.
故选:B.
点评:本题综合考查函数与函数图象,函数的单调性与导数的关系、定积分的几何意义,属于选择题中的高档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列各图中,不能表示函数y=f(x)的图象的是( )
A、 |
B、 |
C、 |
D、 |
数列1,
,
,
,
,
,
,
,
,
,…前130项的和等于( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
A、15
| ||
B、15
| ||
C、15
| ||
D、15
|