题目内容

已知动点M的坐标满足方程5
x2+y2
=|3x+4y-12|，则动点M的轨迹为
 
．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：把已知方程变形为
x2+y2
=
|3x+4y-12|
5
，此式满足抛物线的定义，从而得到答案．
解答： 解：∵动点M的坐标满足方程5
x2+y2
=|3x+4y-12|，变形为
x2+y2
=
|3x+4y-12|
5
，
∴上式表示的是动点M（x，y）到定点（0，0）与定直线3x+4y-12=0的距离相等且定点不在定直线上，
根据抛物线的定义可知：动点的轨迹是以定点为焦点，定直线为准线的一条抛物线．
故答案为：抛物线．
点评：本题考查方程表示的几何意义，注意变形，理解抛物线的定义是解题的前提．
练习册系列答案
相关题目
某地区重视环境保护，绿色植被面积呈上升趋势，经过调查，现有森林面积为10000m2，每年增长10%，经过x年，森林面积为ym2．
（1）写出x，y之间的函数关系式；
（2）求出经过10年后森林的面积．（可借助于计算器）
已知向量
a
，
b
，满足|
a
|=3，|
b
|=2
3
，且
a
⊥（
a
+
b
），则
a
与
b
的夹角为
 
．
设函数f（x）=lnx-ax+
1-a
x
-1．
（1）当a=1时，求曲线f（x）在x=1处的切线方程；
（2）当a=
1
3
时，求函数f（x）的单调区间；
（3）在（2）的条件下，设函数g（x）=x2-2bx-
5
12
，若对于?x1∈[1，2]，?x1∈[0，1]，使f（x1）≥g（x2）成立，求实数b的取值范围．
在△ABC中，已知（b+c）：（c+a）：（a+b）=8：9：10，则sinA：sinB：sinC=
 
．
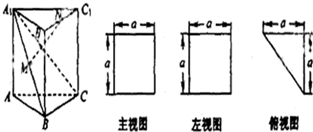一个多面体的直观图和三视图（主观图、左视图、俯视图）如图所示，M、N分别为A1B、B1C1的中点．
（1）求证：MN∥平面ACC1A1；
（2）求证：MN⊥平面A1BC；
（3）求二面角A-A1B-C的大小．
正方形ABCD的边长为1，点M，N分别在线段AB，AD上．若3|MN|2+|CM|2+|CN|2=
9
2
，则|AM|+|AN|的最大值是
 
．
不论m为何值，直线mx-y+2m+1=0恒过的一个定点是
 
．
已知实数x，y，满足约束条件
x≥-1
y≥0
x+y≥1
，则（x+1）2+y2的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网