题目内容
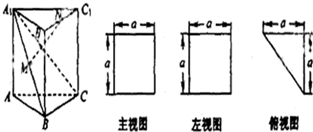一个多面体的直观图和三视图（主观图、左视图、俯视图）如图所示，M、N分别为A1B、B1C1的中点．（1）求证：MN∥平面ACC1A1；
（2）求证：MN⊥平面A1BC；
（3）求二面角A-A1B-C的大小．
考点：二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离,空间角,空间向量及应用
分析：（1）通过已知条件容易判断BC，BA，BB1三条直线两两垂直，所以可建立空间直角坐标系．通过观察MN好像和AC1平行，求向量
，
的坐标，证明两向量平行即可；
（2）在平面A1BC内找从一点出发的两个向量，并求其坐标，分别求和向量
的数量积，数量积为0即可；
（3）容易说明平面AA1B⊥平面CA1B，所以所求二面角为90°．
| MN |
| AC1 |
（2）在平面A1BC内找从一点出发的两个向量，并求其坐标，分别求和向量
| MN |
（3）容易说明平面AA1B⊥平面CA1B，所以所求二面角为90°．
解答：
解：（1）分别以CB，AB，BB1所在直线为x轴，y轴，z轴建立空间直角坐标系．
能确定以下几点坐标：
A（0，-a，0），B（0，0，0），C（-a，0，0），A1（0，-a，a），C1(-a，0，a)，M(0，-
，
)，N(-
，0，a)；
∴
=(-
，
，
)，
=(-a，a，a)，
=(0，a，-a)，
=(-a，a，0)，
=(0，
，
)，
=(a，0，0)；
∴
=
，∴
∥
，∴MN∥AC1，AC1?平面ACC1A1，MN?平面ACC1A1；
∴MN∥平面ACC1A1．
（2）
=(0，-a，a)，
=(-a，0，0)；
∴
•
=-
+
=0，∴
⊥
，∴MN⊥BA1；
同理
⊥
，∴MN⊥BC，BA1∩BC=B；
∴MN⊥平面A1BC；
（3）∵BC⊥AB，BC⊥BB1，AB∩BB1=B；
∴BC⊥平面ABB1A1，即BC⊥平面AA1B；
∴二面角A-A1B-C为直二面角；
∴二面角A-A1B-C的大小为90°．
能确定以下几点坐标：A（0，-a，0），B（0，0，0），C（-a，0，0），A1（0，-a，a），C1(-a，0，a)，M(0，-
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
∴
| MN |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| AC1 |
| A1B |
| A1C1 |
| AM |
| a |
| 2 |
| a |
| 2 |
| CB |
∴
| MN |
| 1 |
| 2 |
| AC1 |
| MN |
| AC1 |
∴MN∥平面ACC1A1．
（2）
| BA1 |
| BC |
∴
| MN |
| BA1 |
| a2 |
| 2 |
| a2 |
| 2 |
| MN |
| BA1 |
同理
| MN |
| BC |
∴MN⊥平面A1BC；
（3）∵BC⊥AB，BC⊥BB1，AB∩BB1=B；
∴BC⊥平面ABB1A1，即BC⊥平面AA1B；
∴二面角A-A1B-C为直二面角；
∴二面角A-A1B-C的大小为90°．
点评：考查空间直角坐标系，两向量垂直的充要条件，线面垂直的判定定理，以及二面角，直二面角．
练习册系列答案
相关题目
