题目内容
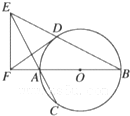如图，AB是⊙O的直径，弦BD、CA的延长线相交于点E，EF垂直BA的延长线于点F．求证．（Ⅰ）∠DEA=∠DFA；
（Ⅱ）AB2=BE•BD-AE•AC．
考点：与圆有关的比例线段
专题：直线与圆
分析：（Ⅰ）连结AD，由已知条件结合圆的性质推导出A、D、E、F四点共圆，由此能证明∠DEA=∠DFA．
（Ⅱ）由A、D、E、F四点共圆，连结BC，能推导出△ABC∽△AEF，由此能证明AB2=BE•BD-AE•AC．
（Ⅱ）由A、D、E、F四点共圆，连结BC，能推导出△ABC∽△AEF，由此能证明AB2=BE•BD-AE•AC．
解答：
证明：（Ⅰ）连结AD，∵AB为圆的直径，∴∠ADB=90°，
又∵EF⊥AB，∴∠EFA=90°，
∴A、D、E、F四点共圆，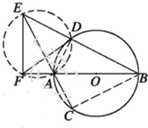
∴∠DEA=∠DFA．
（Ⅱ）∵A、D、E、F四点共圆，
∴由切割线定理知BD•BE=BA•BF，
连结BC，则△ABC∽△AEF，
∴
=
，
∴AB•AF=AE•AC，
∴BE•BD-AE•AC=BA•BF-AB•AF
=AB（BF-AF）=AB2．
∴AB2=BE•BD-AE•AC．
又∵EF⊥AB，∴∠EFA=90°，
∴A、D、E、F四点共圆，
∴∠DEA=∠DFA．
（Ⅱ）∵A、D、E、F四点共圆，
∴由切割线定理知BD•BE=BA•BF，
连结BC，则△ABC∽△AEF，
∴
| AB |
| AE |
| AC |
| AF |
∴AB•AF=AE•AC，
∴BE•BD-AE•AC=BA•BF-AB•AF
=AB（BF-AF）=AB2．
∴AB2=BE•BD-AE•AC．
点评：本题考查两个角相等的证明，考查圆的性质的应用，是中档题，解题时要注意四点共圆的证明及应用．
练习册系列答案
名校课堂系列答案
相关题目
设复数z=
，则复数z2的实部与虚部的和为（ ）
| 2i |
| -1+i |
| A、0 | B、2 | C、-2 | D、4 |
如图所示，ABCDEF是边长为1的正六边形，现从六个顶点任取三个顶点构成三角形，该三角形的面积S是一随机变量．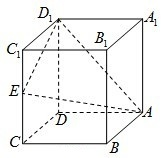
如图，在正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面B1BCC1上的动点，并且A1F∥平面AED1，则动点F的轨迹是（ ）
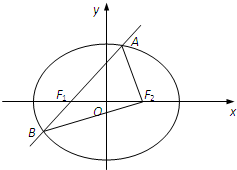如图，椭圆E：