题目内容
 如图所示,ABCDEF是边长为1的正六边形,现从六个顶点任取三个顶点构成三角形,该三角形的面积S是一随机变量.
如图所示,ABCDEF是边长为1的正六边形,现从六个顶点任取三个顶点构成三角形,该三角形的面积S是一随机变量.(1)求S=
| ||
| 2 |
(2)求S的分布列及期望.
考点:离散型随机变量的期望与方差,几何概型
专题:概率与统计
分析:(Ⅰ) 由古典概型的概率计算公式能求出取出的三角形的面积=
的概率.
(Ⅱ) 由题设条S的所有可能取值为
,
,
,分别求出P(S=
),P(S=
),P(S=
),由此能求出随机变量XS的分布列及期望.
| ||
| 2 |
(Ⅱ) 由题设条S的所有可能取值为
| ||
| 4 |
| ||
| 2 |
3
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
3
| ||
| 4 |
解答:
解:(Ⅰ) 由题意得取出的三角形的面积=
的概率
P=
=
.
(Ⅱ) 由题设条S的所有可能取值为
,
,
,
P(S=
)=
=
,
P(S=
)=
=
,
P(S=
)=
=
,
∴随机变量XS的分布列为:
ES=
×
+
×
+
×
=
.
| ||
| 2 |
P=
| 12 | ||
|
| 3 |
| 5 |
(Ⅱ) 由题设条S的所有可能取值为
| ||
| 4 |
| ||
| 2 |
3
| ||
| 4 |
P(S=
| ||
| 4 |
| 6 | ||
|
| 3 |
| 10 |
P(S=
| ||
| 2 |
| 12 | ||
|
| 3 |
| 5 |
P(S=
3
| ||
| 4 |
| 2 | ||
|
| 1 |
| 10 |
∴随机变量XS的分布列为:
| S |
|
|
| ||||||||||||
| P |
|
|
|
| ||
| 4 |
| 3 |
| 10 |
| ||
| 2 |
| 3 |
| 5 |
3
| ||
| 4 |
| 1 |
| 10 |
9
| ||
| 20 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
在四面体ABCD中,已知AB=x,该四面体的其余五条棱的长度均为2,则下列说法中错误的是( )
A、棱长x的取值范围是:0<x<2
| ||
| B、该四面体一定满足:AB⊥CD | ||
C、当x=2
| ||
| D、当x=2时,该四面体的体积最大 |
 如图,在△ABC中,已知AB=10,AC=14,B=
如图,在△ABC中,已知AB=10,AC=14,B=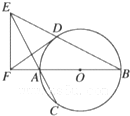 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.