题目内容
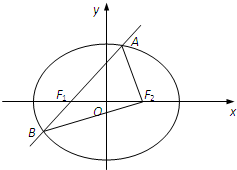 如图,椭圆E:
如图,椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q,证明:点M(1,0)在以PQ为直径的圆上.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)已知△ABF2的周长为8,即4a=8,求得a,再由△AF1F2面积最大时,△AF1F2为正三角形可得椭圆的离心率,则c可求,进一步求得b,则椭圆方程可求;
(2)联立直线和椭圆方程,化为关于x的一元二次方程后由判别式等于0得到k与m的关系,从而求得直线与椭圆的公共点的坐标,再由直线y=kx+m与x=4联立求得Q的坐标,然后利用取特殊值法求得以PQ为直径的圆与x轴的交点坐标,进一步证明
•
=0得答案.
(2)联立直线和椭圆方程,化为关于x的一元二次方程后由判别式等于0得到k与m的关系,从而求得直线与椭圆的公共点的坐标,再由直线y=kx+m与x=4联立求得Q的坐标,然后利用取特殊值法求得以PQ为直径的圆与x轴的交点坐标,进一步证明
| MP |
| MQ |
解答:
解:(1)∵过F1的直线交椭圆于A、B两点,且△ABF2的周长为8,
∴4a=8,a=2.
∵△AF1F2面积最大时,△AF1F2为正三角形,
∴e=
,即
=
,
∴c=1,
∴b2=a2-c2=3.
∴椭圆E的方程为
+
=1;
(2)由
,消元可得(4k2+3)x2+8kmx+4m2-12=0.
∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0),
∴m≠0,△=0,
∴(8km)2-4×(4k2+3)×(4m2-12)=0.
∴4k2-m2+3=0.
此时x0=-
=-
,y0=
,
即P(-
,
)
由
,得Q(4,4k+m).
取k=0,m=
,此时P(0,
),Q(4,
),
以PQ为直径的圆为(x-2)2+(y-
)2=4,交x轴于点M1(1,0)或M2(3,0).
取k=-
,m=2,此时P(1,
),Q(4,0),
以PQ为直径的圆为(x-
)2+(y-
)2=
,交x轴于点M3(1,0)或M4(4,0).
故若满足条件的点M存在,只能是M(1,0),
证明如下∵
=(-
-1,
),
=(3,4k+m),
∴
•
=-
-3+
+3=0
故以PQ为直径的圆恒过y轴上的定点M(1,0).
∴4a=8,a=2.
∵△AF1F2面积最大时,△AF1F2为正三角形,
∴e=
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
∴c=1,
∴b2=a2-c2=3.
∴椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)由
|
∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0),
∴m≠0,△=0,
∴(8km)2-4×(4k2+3)×(4m2-12)=0.
∴4k2-m2+3=0.
此时x0=-
| 4km |
| 4k2+3 |
| 4k |
| m |
| 3 |
| m |
即P(-
| 4k |
| m |
| 3 |
| m |
由
|
取k=0,m=
| 3 |
| 3 |
| 3 |
以PQ为直径的圆为(x-2)2+(y-
| 3 |
取k=-
| 1 |
| 2 |
| 3 |
| 2 |
以PQ为直径的圆为(x-
| 5 |
| 2 |
| 3 |
| 4 |
| 45 |
| 16 |
故若满足条件的点M存在,只能是M(1,0),
证明如下∵
| MP |
| 4k |
| m |
| 3 |
| m |
| MQ |
∴
| MP |
| MQ |
| 12k |
| m |
| 12k |
| m |
故以PQ为直径的圆恒过y轴上的定点M(1,0).
点评:本题椭圆方程的求法,考查直线与椭圆的位置关系的应用,体现了数学转化思想方法,训练了特值化思想在解题中的应用,考查了计算能力,是高考试卷中的压轴题.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
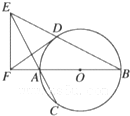 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.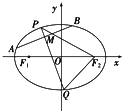 已知椭圆C:
已知椭圆C: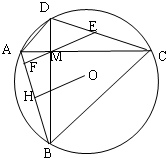 如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证:
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证: