题目内容
已知集合A={x|mx-1=0},B={x∈Z|2x2+x≤0},若A∩B=A,则满足条件的实数m的值为 .
考点:集合的包含关系判断及应用
专题:集合
分析:本题的关键是高清集合A、B的元素,对于集合A,需要分情况讨论.再利用集合A、B的包含关系求出m的值
解答:
解:∵A={x|mx-1=0}
∴当m=0时,A=Φ
当m≠0时,A={
}
又∵B={x∈Z|2x2+x≤0},
∴B={0}
∵A∩B=A
∴A⊆B
∴m=0时,A=Φ⊆B,成立
m≠0时,
=0,m无解.
综上,m=0
故答案为:m=0
∴当m=0时,A=Φ
当m≠0时,A={
| 1 |
| m |
又∵B={x∈Z|2x2+x≤0},
∴B={0}
∵A∩B=A
∴A⊆B
∴m=0时,A=Φ⊆B,成立
m≠0时,
| 1 |
| m |
综上,m=0
故答案为:m=0
点评:本题主要考查集合的基本运算,属于基础题.要正确判断两个集合的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征.

练习册系列答案
相关题目
已知函数f(x)为奇函数,且当x<0时,f(x)=x2+2x,则f(1)=( )
| A、1 | B、-1 | C、3 | D、-3 |
下列关于两条不同的直线l,m两个不重合的平面α,β的说法,正确的是( )
| A、若l?α且α⊥β,则l⊥β |
| B、若l⊥β且m⊥β,则l∥m |
| C、若l⊥β且α⊥β,则l∥α |
| D、若α∩β=m且l⊥m,则l⊥α |
已知全集U={x∈Z|1≤x≤5},A={1,2,3},∁UB={1,2},则A∩B( )
| A、{1,2} |
| B、{1,3} |
| C、{3} |
| D、{1,2,3} |
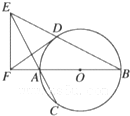 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.
如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.求证.